Readability in proofs: the mean value theorem
[examples analysis Isar Doing mathematics requires a combination of intuition and rigour. Intuition is the source of ideas and conjectures. Proofs need to be rigorous, while at the same time avoiding excessive detail, which would destroy readability. That is why we need intuition even to read a proof, let alone to conceive the theorem in the first place. How can we capture intuition in a formal proof?
The mean value theorem
Our example, the mean value theorem, is an elementary fact about the differential calculus:
- If $\phi(x)$ is continuous in the closed interval $[a,b]$, and differentiable in the open interval, then there is a value $\xi$ of $x$ between $a$ and $b$, such that $\phi(b)-\phi(a) = (b-a)\phi’(\xi)$.
GH Hardy, in his legendary Pure Mathematics (CUP, 1952), begins as follows (p. 242):
Before we give a strict proof of this theorem, which is one of the most important theorems in the differential calculus, it will be well to point out its obvious geometrical meaning. This is simply that, if the curve $APB$ has a tangent at all points of its length, then there must be a point, such as $P$, where the tangent is parallel to $AB$. For $\phi’(\xi)$ is the tangent of the angle which the tangent at $P$ makes with $OX$, and $(\phi(b) - \phi(a))/(b - a)$ the tangent of the angle which $AB$ makes with $OX$.
Here is Hardy’s accompanying diagram:
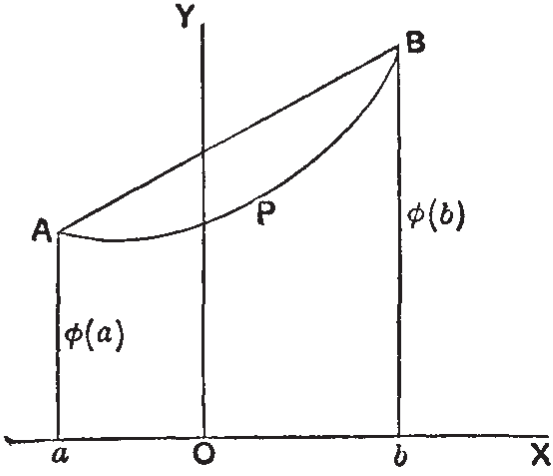
Hardy continues:
It is easy to give a strict proof. Consider the function
\[\phi(b) - \phi(x) - \frac{b-x}{b-a}(\phi(b)-\phi(a))\]
which vanishes when $x = a$ and $x = b$. It follows from [Rolle’s Theorem] that there is a value $\xi$ for which its derivative vanishes. But this derivative is
\[\frac{\phi(b)-\phi(a)}{b-a} - \phi'(x)\]
which proves the theorem.
The proof in the Isabelle/HOL library is slightly different, defining a function f that does not actually vanish (no need for that) and its derivative has the opposite sign. Nevertheless, the formal proof contains essentially the same application of Rolle’s theorem.
The MVT formalised in Isabelle/HOL
The Isabelle proof rewards closer inspection. The theorem’s assumptions include $a<b$ and the continuity and differentiability conditions on $\phi$. If you recall the earlier post on undefined values, you’ll understand why differentiability is expressed by a relation that actually names the derivative as $\phi’$. The conclusion of the theorem asserts that we “obtain” some $\xi$ satisfying the required properties. The obtains keyword is one way to express an existential conclusion.
theorem mvt: fixes φ :: "real ⇒ real" assumes "a < b" and contf: "continuous_on {a..b} φ" and derf: "⋀x. ⟦a < x; x < b⟧ ⟹ (φ has_derivative φ' x) (at x)" obtains ξ where "a < ξ" "ξ < b" "φ b - φ a = (φ' ξ) (b-a)" proof - define f where "f ≡ λx. φ x - (φ b - φ a) / (b-a) * x" have "∃ξ. a < ξ ∧ ξ < b ∧ (λy. φ' ξ y - (φ b - φ a) / (b-a) * y) = (λv. 0)" proof (intro Rolle_deriv[OF ‹a < b›]) fix x assume x: "a < x" "x < b" show "(f has_derivative (λy. φ' x y - (φ b - φ a) / (b-a) * y)) (at x)" unfolding f_def by (intro derivative_intros derf x) next show "f a = f b" using assms by (simp add: f_def field_simps) next show "continuous_on {a..b} f" unfolding f_def by (intro continuous_intros assms) qed then show ?thesis by (smt (verit, ccfv_SIG) pos_le_divide_eq pos_less_divide_eq that) qed
In the proof we see the f being defined for use with Rolle’s theorem, whose conditions are then proved. The conclusion follows by simple algebra. Our exposition is not as clear as Hardy’s, but we see how f is defined and what its crucial properites are. This proof, being machine-checked, is rigorous, while retaining a bit of intuition: we don’t have to spell out any more detail.
Looking closer at the proof justifications, we see multiple uses of the intro method to prove differentiability and continuity of f. The smt justification was generated automatically by Sledgehammer.
Postscript
GH Hardy’s textbook Pure Mathematics is aimed at first-year mathematics undergraduates. It covers analysis up to “the general theory of the logarithmic, exponential, and circular functions”. Hardy’s Preface states “I regard the book as being really elementary.” First published in 1908, it has gone through ten editions and is still in print.
The file containing the MVT example is available to download.