Machine Logic

Proving the obvious

12 Jan 2022

It is commonly opined that proof assistants are useless for mathematics because they are too difficult to learn and use. This opinion is incorrect: I am as skilled as anyone on the planet at using Isabelle/HOL, but no amount of skill can compensate for the limitations of today’s tools. They are simply too stupid to prove obvious things.

The mutilated chessboard

The canonical example of an obvious question asks whether this mutilated chessboard can be tiled by 32 dominoes:

Obviously it can’t be, as seen by the colours of the squares. But perhaps this is a poor example because it is about everyday objects. By the time we’ve translated it into a problem about mathematical objects such as matrices, it’s already game over. Many have tried, including myself, but the amount of work required looks ridiculous. I’ve also seen furious arguments about whether the chessboard was formalised too abstractly.

Triangles in a tripartite graph

So here is a proper mathematical example, from a proof of Roth’s theorem on arithmetic progressions. The proof involves a tripartite graph with sets of vertices $X$, $Y$ and $Z$ (disjoint copies of the integers modulo some $M$). There are edges between these vertex sets but none within them. We are concerned with triangles: three vertices connected by three edges. It’s obvious that every triangle has a vertex in each of the three sets.

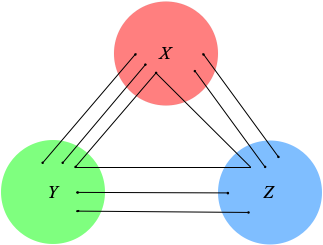
When a claim is really trivial, it can be difficult to come up with an explanation: how low do we have to go? Here we could reason as follows: look at one edge of the given triangle, which we can assume WLOG connects $X$ with $Y$. (Without loss of generality is a problem for theorem provers, and although our graph is undirected, in a syntactic sense there are still six cases.) Because there are no edges within any of the vertex sets, the next edge must connect to either $X$ or $Z$, and if the former, we would be unable to find a third edge for our triangle. BFD. (BFD is preferred to QED when the proof is trivial.)

The argument above is easy to supply to Isabelle/HOL, but it generates hundreds of cases. All of them are trivial enough to prove automatically, but the runtime is intolerable. A certain amount of creativity and perhaps programming skill is required simply to prove (efficiently!) that every triangle consists of a vertex from each of $X$, $Y$ and $Z$ in that order. And that tiresome work comes before we reach any of the serious reasoning in the proof. Ironically, sometimes the difficult calculations elaborately laid out by the author can be proved with less effort than the trivial claims.

A trivial fact about derivatives

The following example came up while formalising a bit of analytic number theory. Suppose that the function $f$ is differentiable at $z$ and that $\sigma_n$ is a series of nonzero reals converging to 0. Then we have

I still wonder why this needs to be proved. It closely resembles the definition of the derivative, and certainly the text gave no hint that a proof was required. But a full $\epsilon$-$\delta$ argument is called for.

lemma field_derivative_lim_unique:
  assumes f: "(f has_field_derivative df) (at z)"
      and s: "s ⇢ 0"  "⋀n. s n ≠ 0" 
      and a: "(λn. (f (z + s n) - f z) / s n) ⇢ a"
    shows "df = a"
proof (rule ccontr)
  assume "df ≠ a"
  obtain q where qpos: "⋀ε. ε > 0 ⟹ q ε > 0" 
             and q: "⋀ε y. ⟦ε > 0; y ≠ z; dist y z < q ε⟧ ⟹ dist ((f y - f z) / (y - z)) df < ε"
    using f unfolding LIM_def has_field_derivative_iff by metis
  obtain NA where NA: "⋀ε n. ⟦ε > 0; n ≥ NA ε⟧ ⟹ dist ((f (z + s n) - f z) / s n) a < ε" 
    using a unfolding LIMSEQ_def by metis
  obtain NB where NB: "⋀ε n. ⟦ε > 0; n ≥ NB ε⟧ ⟹ norm (s n) < ε" 
    using s unfolding LIMSEQ_def by (metis norm_conv_dist)
  have df: "⋀ε n. ε > 0 ⟹ ⟦0 < ε; norm (s n) < q ε⟧ ⟹ dist ((f (z + s n) - f z) / s n) df < ε"
    using add_cancel_left_right add_diff_cancel_left' q s
    by (metis add_diff_cancel_right' dist_diff(1))
  define δ where "δ ≡ dist df a / 2"
  with ‹df ≠ a› have "δ > 0" and δ: "δ+δ ≤ dist df a"
    by auto
  define N where "N ≡ max (NA δ) (NB (q δ))"
  then have "norm (s N) < q δ"
    by (simp add: NB ‹δ > 0› qpos)
  then have "dist ((f (z + s N) - f z) / s N) df < δ"
    by (simp add: ‹0 < δ› df)
  moreover have "dist ((f (z + s N) - f z) / s N) a < δ"
    using NA N_def ‹0 < δ› by force
  ultimately have "dist df a < dist df a"
    by (smt (verit, ccfv_SIG) δ dist_commute dist_triangle)
  then show False ..
qed

The theorem statement seems to assert the uniqueness of the derivative. However, theorems to this effect already exist in the Isabelle/HOL library and don’t appear to help. If you can see a more direct way of proving this result please send it along and I will highlight it in a future post.

Further examples

These examples, as well as the previous one, come from Modular Functions and Dirichlet Series in Number Theory by Tom M. Apostol. He remarks that it “evolved from a course … offered at the California Institute of Technology during the last 25 years,” so it represents mathematics as it is taught in a first-rate institution.

Theorem 1.5. If an elliptic function $f$ has no zeros in some period parallelogram, then $f$ is constant.

PROOF. Apply Theorem 1.4 to the reciprocaI $1/f$. $\qquad\Box$

The Isabelle/HOL proof is more than 60 lines long.

Theorem 1.6. The contour integral of an elliptic function taken along the boundary of any cell is zero.

PROOF. The integrals along parallel edges cancel because of periodicity. $\qquad\Box$

The Isabelle/HOL proof is more than 100 lines long.

Theorem 1.7. The sum of the residues ofan ellipticfunction at its poles in any period parallelogram is zero.

PROOF. Apply Cauchy’s residue theorem to a cell and use Theorem 1.6. $\qquad\Box$

The Isabelle/HOL proof is nearly 200 lines long.

Each of these claims has a one-sentence proof, but their formal proofs are long and complicated, the work of several highly talented people. So either the proofs are trivial and proof assistants have a long way to go, or perhaps, Apostol simply could not be bothered to prove his claims. I am not qualified to judge. What do you think?