On Turing machines
[general logic Alan Turing Kurt Gödel Ackermann's function Every now and then, somebody claims that Turing “invented the computer”, because he invented Turing machines. However, Turing machines are not designs of actual computing machines. They aren’t even abstract models of machines. It turns out (we have Turing’s own word for it), a TM is a model of a man writing on paper at a desk. So why did Turing invent TMs, and where did this lead?
Turing’s article “On Computable Numbers”
It’s often best to put your textbooks aside and turn to the papers themselves. These days there is no need to fill out a borrowing card for a journal volume dated 1936 and wait an hour or so for the librarian to fetch it from storage. Just ask Mr Google while relaxing at home, a glass of single malt at your side. Turing’s paper can be found online (also here). It is a wonderful read, even with its mistakes: as Joel David Hamkins explains, Turing’s definition of computable real numbers as those having computable decimal expansions doesn’t actually work, though a fix is not difficult.
Turing states his intentions right in the title: “On Computable Numbers, with an Application to the [Decision Problem]”. (The Entscheidungsproblem asks whether there exists an effective technique for determining whether a given formula of first-order logic is valid, i.e., true in all interpretations.) Turing expands on his thinking as follows:
We may compare a man in the process of computing a real number to a machine which is only capable of a finite number of conditions $q_1$, $q_2$, … $q_R$ … . The machine is supplied with a “ tape” (the analogue of paper) running through it, and divided into sections (called “squares”) each capable of bearing a “ symbol”. … Some of the symbols written down will form the sequence of figures which is the decimal of the real number which is being computed. The others are just rough notes to “assist the memory”. It will only be these rough notes which will be liable to erasure. It is my contention that these operations include all those which are used in the computation of a number.
Turing proceeds with definitions and proofs, typical of a mathematics article and not at all typical of an engineering article, where one would expect to see a discussion of how to realise some mechanism that had been described. Turing’s main concern, as we see both from his title and from the passage quoted above, is the computation of a single real number to an unlimited number of decimal places.
The paper makes many other fundamental contributions:
- the universal machine, and with it the idea of coding machines in the form of numbers
- the halting problem (not exactly!) for machines so coded, and its undecidability by diagonalisation
And much more. Turing, in this one paper, launched the field of theoretical computer science.
On the universal machine
We can’t be sure what put Turing on to the idea of a universal machine, but once he thought of it, he probably thought that its existence was obvious. Since the very point of a TM was to simulate a clerk working at a desk, and the operation of a TM was itself clerical—depending on the machine state and tape symbol, do this or do that as directed by a given list of transition rules—there was obviously a TM to carry out such a routine task. Turing’s paper is a bit sketchy about how the details of the constrution, but it seems that nobody minded. (After all, Gödel never did get around to publishing any proof of his second incompleteness theorem; people thought it obvious, although the details turned out to be fiendish.)
Today we have universal machines that have been worked out to the last detail. Here at Cambridge, decades ago, Dr Ken Moody felt the itch to “hack”, so he coded a universal Minsky register machine. Such a machine has finitely many registers, each of which can hold an arbitrarily large non-negative integer. It has a finite program consisting of labelled instructions, of three different kinds:
- increment register $R$ and jump to label $L$, or $R^{+}\to L$
- test/decrement register $R$ and jump to label $L_0$/$L_1$, or $L_0 \twoheadleftarrow R^{-}\to L_1$
- halt.
They are easier than Turing machines to program, although they still don’t resemble real computers.
Moody used a standard bijection between $\mathbb{N}$ and $\mathbb{N}\times\mathbb{N}$ to pack lists of integers into a single integer. He coded a small library of little register machines to perform operations such as push on stack and pop from stack and created a design reminiscent of the fetch-execute cycle of a real processor. The whole thing fits on a couple of slides. Here’s the machine itself:
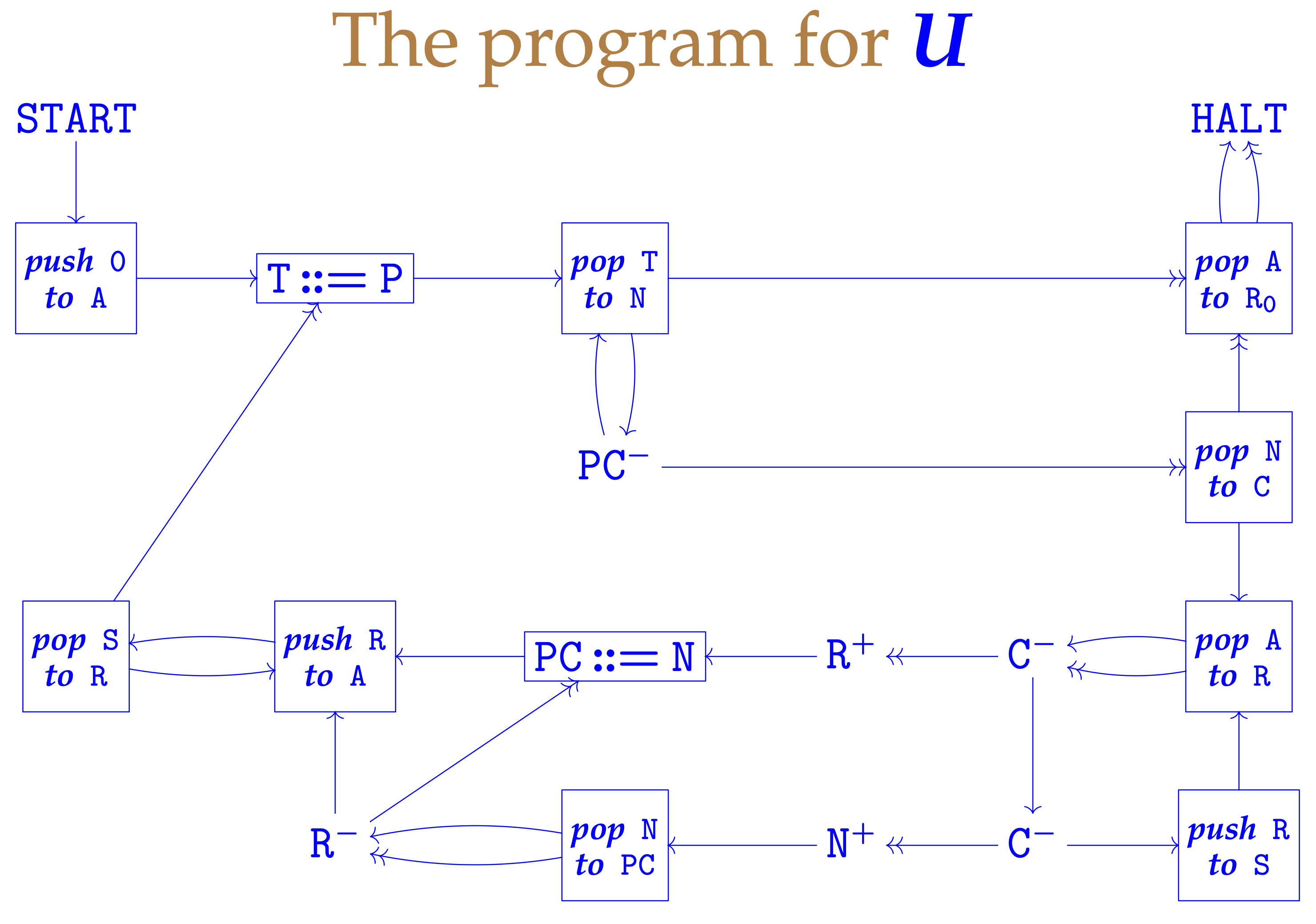
And here’s a brief explanation. (Both of these slides are due to Andrew Pitts.)

Astonishing how simple it is!
On the halting (oops, circularity!) problem
The halting problem is obviously undecidable. Otherwise, many mathematical conjectures would be trivial to resolve, such as Fermat’s last theorem: just write a program to search for $x$, $y$, $z$, $n>2$ such that $x^n+y^n = z^n$ and ask whether it terminates. Nevertheless, the undecidability claim has to be rigorously expressed and proved.
Contrary to popular belief, Turing’s paper does not address the halting problem, but a related property that he calls circularity. A TM is circular provided it “never writes down more than a finite number of symbols of the first kind” (zeros and ones). Circularity mattered, I suppose, because of Turing’s specific interest in approximating real numbers as infinite binary strings. Christopher Strachey claimed, in a 1965 Letter to the Computer Journal, that Turing informed him of a proof of the undecidability of the actual halting problem.

Turing and Maurice Wilkes
For a contrarian opinion of Turing, here is Maurice Wilkes, interviewed by David P. Anderson:
Looking back, what would you say was the significance of Turing’s 1936 Entscheidungs-problem paper?
I always felt people liked to make a song and dance. Something like the doctrine of the Trinity involved whereas to an engineer you’ve only got to be told about the stored program idea and you’d say at once “That’s absolutely first-rate, that’s the way to do it.” That was all there was to know.
There was no distinction in that paper that had any practical significance. He was lucky to get it published at all but I’m very glad he did. I mean [Alonzo] Church had got the same result by other methods.
WTF? Well, Wilkes was 96 at the time of this interview, and himself a notable computer pioneer, the father of the EDSAC. In his bizarre answer we see perhaps his jealousy of Turing’s iconic status. The two men clearly didn’t get along! We also see Wilkes’s lifelong disdain for theory: though the idea of coding machines as numbers anticipates the stored-program computer, Turing’s work here is purely mathematical, having no engineering implications whatever. Turing was interested in the engineering of actual computers, but his attempts to get involved were repeatedly frustrated.
And what about those remarks about Church?
Turing and Church at Princeton
Turing was working at the exact moment that many researchers were converging on the idea of “effective calculability”. In keeping with my suggestion to read the original papers, let me recommend Church’s An Unsolvable Problem of Elementary Number Theory. To be honest, it is a tough read, but it puts you into the context of the time. Here we find a definition of the $\lambda$-calculus, a definition of recursive function (in the sense of Kleene/Gödel) and some undecidability results for the existence and equivalence of normal forms in the $\lambda$-calculus. Church and Kleene had already proved the equivalence of the $\lambda$-definable functions and recursive functions; during Turing’s time at Princeton, the equivalence between the $\lambda$-definable functions and the Turing-computable was also proved, establishing the Church-Turing thesis: that the effectively computable functions are precisely the functions in those mathematically equivalent classes.
Is the Church-Turing thesis true?
As is often remarked, this claim cannot be proved because “effectively computable” is not a precise concept. The Turing-computable functions can be regarded as a generous class because they include many functions that cannot be computed within the lifetime of the universe. Examples are easily produced with the help of Ackermann’s function. If you define $f(n) = A(n,n)$, you cannot hope to compute even $f(4)$. And $g(n) = A(4,n)$ is all but impossible to compute despite being primitive recursive.
Although there were no digital computers until at least the 1930s, the idea of effective computability was well known to mathematicians. The idea of effectiveness was already present in the straightedge and compass constructions of Greek geometry, and it is also part of the formulation of the Entscheidungsproblem and Hilbert’s tenth problem. The genius of Turing’s conception, compared with Gödel’s recursive functions and Church’s $\lambda$-calculus, is that it is obviously right. Gödel himself was not sure whether his recursive functions captured the idea of computation, nor was it clear that Church had the right idea. Turing’s was simple and natural. That it was provably equivalent to those other models provided justification for all of them. He published that fact in his 1937 paper, “Computability and λ-definability”.
The purpose of the present paper is to show that the computable functions introduced by the author are identical with the $\lambda$-definable functions of Church and the general recursive’ functions due to Herbrand and Gbdel and developed by Kleene. It is shown that every X-definable function is computable and that every computable function is general recursive.
Note that Turing writes “computable” where we would write “Turing computable”. Wikipedia has a useful chronology of those events.
These days, computation is typically interwoven with communication, and none of these models of computation have anything to say about that. Unfortunately, the numerous models we have of concurrent computation do not turn out to be equivalent. The situation regarding models of concurrency remains messy.
Postscript: I would like to thank Ken Moody and Andrew Pitts for their helpful remarks.
Postscript added November 2024: See also the paper Did Turing Prove the Undecidability of the Halting Problem?, by Hamkins and Nenu. They note that Turing also proved the undecidability of what they call the symbol-printing problem: it is closely related to the halting problem, although Turing’s proof is like nothing given today.