MetiTarski: an automatic prover for real-valued special functions
[MetiTarski Way back when I first discussed interactive theorem proving with Mike Gordon, nearly 40 years ago, I wondered aloud whether we would ever see the formalisation of a really deep result in mathematics, such as the prime number theorem. It happened in 2004, when Jeremy Avigad formalised an elementary proof of the theorem (meaning, a proof not reliant on complex analysis) using Isabelle/HOL. (Paper also on ArXiv.) Jeremy remarked that he had spent an inordinate amount of time proving trivial inequalities involving the log function; he wrote a proposal on how such proofs might be automated, and eventually an implementation. I had my own ideas, and being lucky enough to live in an era when research grants could be awarded for crazy ideas, got funding to provide such automation as an extension to Isabelle/HOL. But things turned out differently and we ended up with a stand-alone automatic theorem prover, MetiTarski.
Upper and lower bounds for special functions
Much of the groundwork was laid by my capable and dedicated postdoc, Behzad Akbarpour. It was he, I believe, who stumbled upon a paper by César Muñoz and David Lester entitled “Real Number Calculations and Theorem Proving”. This paper (and not the one with the same name that appeared in the same conference three years later) outlined an approach to dealing with complicated arithmetic expressions involving trigonometric functions and whatever, within automated theorem proving. The idea was to reason about functions such as $\sin$ and $\ln$ in terms of using interval arithmetic to bound their possible values. Each occurrence of a function would be replaced by a polynomial approximation that was either an upper bound or a lower bound. The paper actually supplied systems of bounds for the most important of the so-called special functions: $\sin$, $\cos$, $\ln$, square roots and exponentials, etc.
Our first experiments were conducted through hand calculations. We quickly discovered that interval arithmetic was too crude a tool to solve our target problems (which at first were those suggested by Jeremy). We needed a more powerful technology.
Real-closed fields
Most people in our field are aware that the theory of linear arithmetic is decidable: algorithms exist to decide Boolean combinations of inequalities involving addition and subtraction but with multiplication and division only by constants. Actually, something much stronger is true: if all variables range over the real numbers, arbitrary logical formulas with unrestricted multiplication and quantification are decidable. Although the algorithms for this are necessarily hyper-exponential, the worst case complexity of the decision procedures for linear arithmetic isn’t great either.
Anyway, we decided to try our luck with some RCF decision procedures. We first used an implementation by McLaughlin and Harrison of a procedure due to Hörmander, with some success. Further work showed the limitations of that decision procedure because some of our polynomial approximations were of too high degree. QEPCAD, a stand-alone tool implementing a more powerful decision procedure (cylindrical algebraic decomposition) gave much better results. We published our findings using QEPCAD a year later (2008).
Resolution theorem proving
As mentioned above, the basic approach was to take a given inequality involving special functions and then
- replace function occurrences by polynomials (lower or upper bounds, as appropriate)
- to eliminate any occurrences of division
- to solve the remaining polynomial inequalities using QEPCAD.
One could imagine writing a lot of code to perform these tasks. Whether through laziness or inspiration, I decided to give the task to a resolution theorem prover. Surrendering control over the heuristic process to an automatic procedure has both advantages and drawbacks, but it meant that the upper/lower bounds could be supplied in the form of axioms; these could have arbitrary logical conditions to describe their domain of validity. If a particular problem involved the use of multiple lower bounds for the same function over partially overlapping domains, dealing with such complications would be the responsibility of the general automation provided by resolution. The elimination of division in favour of multiplication can also be performed simply by stating the mathematical justification in the form of axioms. And problems could involve logical connectives.
Nevertheless, the resolution prover would need to be augmented with problem specific knowledge. In particular, arithmetic expressions would need to be simplified to a canonical form since otherwise the numerous variants of any expression would be overwhelming. It also need to be integrated with QEPCAD, but that turned out to be easy: any clause that happened to contain a ground algebraic formula could be converted into a QEPCAD problem such that if QEPCAD detected a contradiction, the corresponding literal of that clause would be deleted. Certain other low-level modifications of the proof process would guide its heuristics to “zero in” on proofs in our particular domain.
Most resolution theorem provers are giant incomprehensible mountains of C or C++, but luckily, I was able to use Metis, an exceptionally clean implementation of superposition by Joe Leslie-Hurd and coded in Standard ML. My team modified Metis more and more over the years, especially with the award of a follow-up grant. Another postdoc, James Bridge, implemented some highly ambitious extensions, including case splitting, which was appropriate because of the large numbers of ground literals generated by our approach. We repeatedly extended the set of special functions that we could support and continued to improve the performance.
Examples
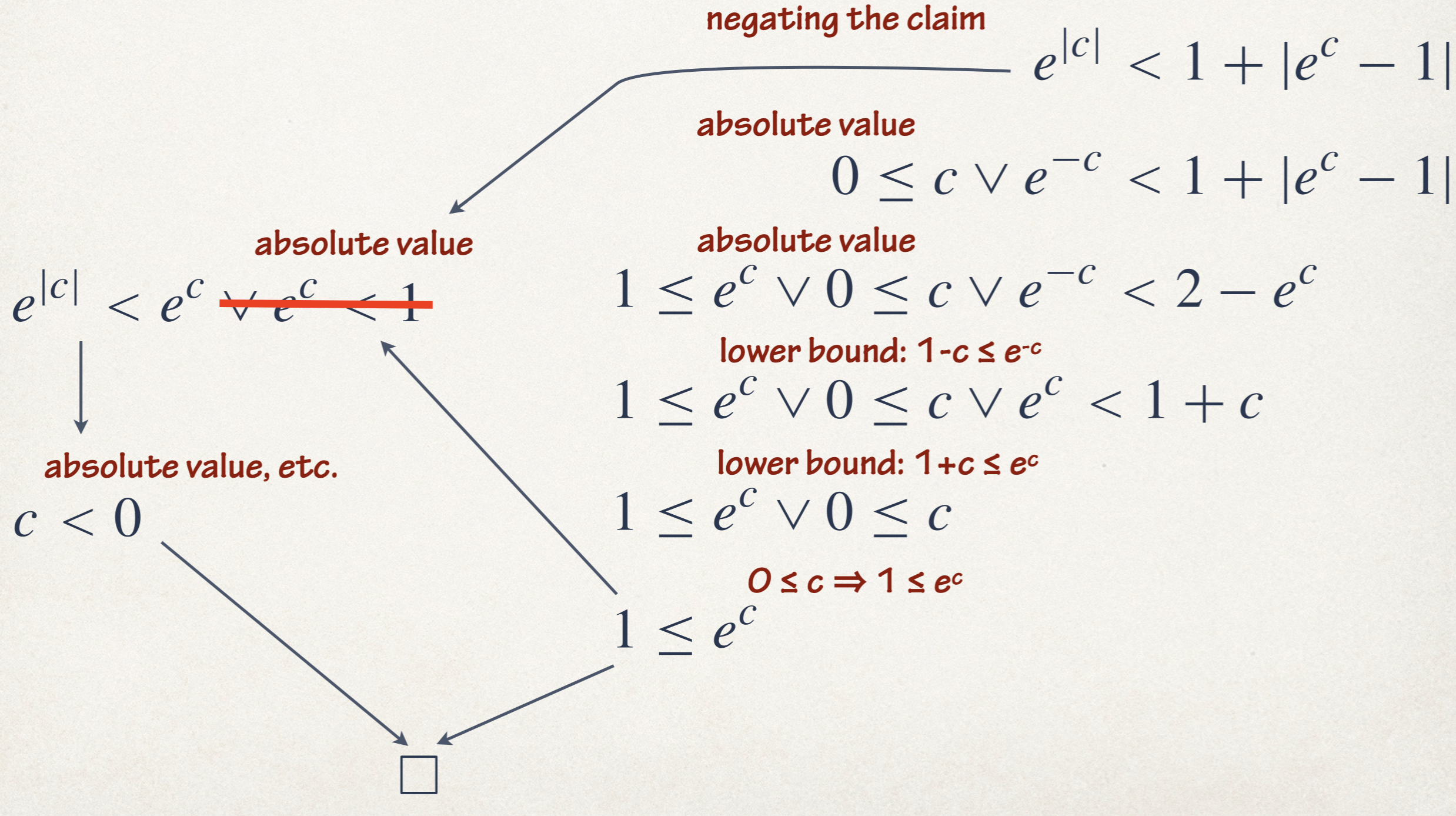
For starters, let’s look at the proof of $\forall x\,\lvert e^x-1\rvert\le e^{\lvert x \rvert}-1$. To keep the diagram small, many steps have been skipped, above all those in which an axiom is used to replace a function by an upper/lower bound. The absolute value function is dealt with by essentially a case analysis.
Here are the statements of four more small examples.
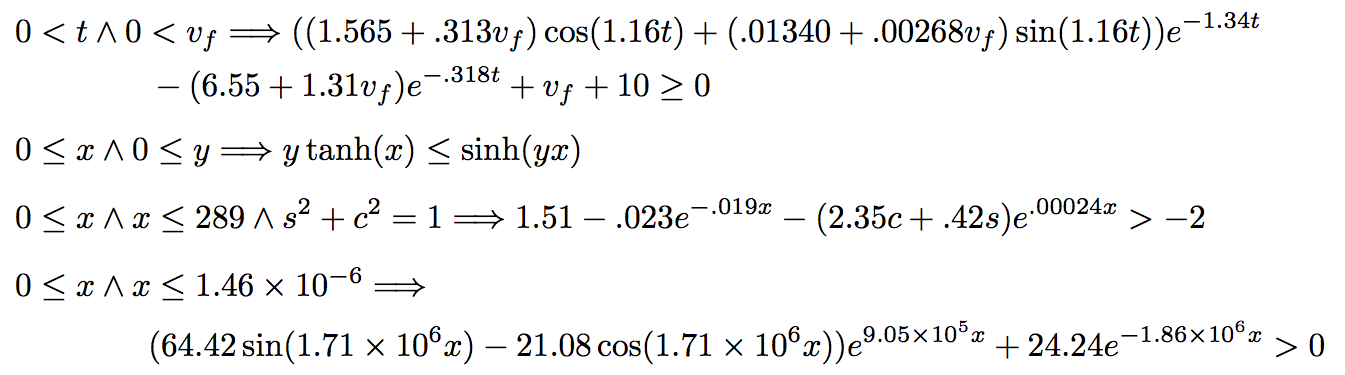
The generated proofs are typically on the order of hundreds of steps long and one can work through them by hand, with patience. The reasoning is often contorted, particularly in cases where multiple bounds need to be used in order to cover the entire range of a given variable.
The problem set for MetiTarski gradually grew from a few dozen problems suggested by Jeremy to a collection of hundreds drawn from various specialised handbooks of inequalities. The main problem set now stands at nearly 900, but thousands of other problems been generated in applications ranging from hybrid systems to floating-point algorithms. The vast majority are solved in under a second, and MetiTarski outputs a proof in its extended resolution calculus.
Continued fractions
After presenting the 2008 paper at CICM in Birmingham, I met Annie Cuyt, who stated that continued fractions would yield upper/lower bounds far superior than the ones I was using, which were mostly based on Taylor expansions. She referred me to her then recent Handbook of Continued Fractions and the associated library for the computer algebra system Maple. She was right: continued fraction bounds turned out to be much better except for sines and cosines, for which Taylor series are best. The definitive paper on MetiTarski, published in 2010, presents the continued fraction bounds.
The Future?
I perhaps naïvely imagined that the capability to solve problems of the sort shown here would have numerous applications. There have been a few, but MetiTarski has definitely not caught on the way Isabelle has. Its most serious limitation perhaps is that only a few variables can be allowed. This limitation is caused by the RCF solvers; Mathematica and Z3 can be substituted for QEPCAD, each with their own benefits and drawbacks. I also had the idea of trying to integrate MetiTarski with Isabelle. I have verified all the upper and lower bounds using Isabelle. Nevertheless, integrating the two systems would involve an enormous amount of work, and the benefits would not be clear.
I still hope that somebody will find a terrific application of this technology.
Acknowledgement. My thanks to the EPSRC for funding this research. It’s a pity that this sort of research doesn’t seem to attract funding any more. And I’m grateful to my numerous colleagues who contributed so much.