Formalising a new proof that the square root of two is irrational
[examples newbies Isar Recently, somebody shared on Twitter a new proof of the irrationality of √2. Its claimed advantage is that “it requires no knowledge of mathematics above the definition of what it means for a number to be irrational, and can be written almost in one line.” These claims are dubious: the usual proof, which I’ve formalised in a previous post, requires only the natural numbers and the notion of divisibility. The “beautiful” proof involves real numbers, potentially infinite sets and the nontrivial claim that the square root of two actually exists. Nevertheless, formalising it in Isabelle/HOL is an interesting exercise. In particular, it illustrates reasoning about the least element of a set. So here we go.
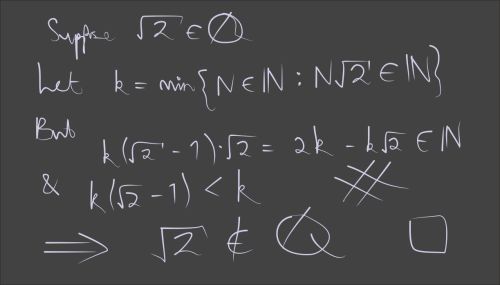
A remark about numeric types
Before we begin, it’s necessary to explain the meanings of the symbols ℕ, ℤ, ℚ, ℝ
in Isabelle/HOL. They denote sets, not types: namely, they denote the sets of natural numbers,
integers, rationals, real numbers (respectively) as images embedded in some larger type.
Here we are mostly going to work within type real, where ℕ and ℚ
will denote sets of real numbers. Through the magic of type classes,
these symbols denote the right set for other types, such as complex,
quaternions
and any other types (including those yet to be defined) that inherit the necessary structure.
We need to be careful with types here. I’ve used the function real, which injects natural numbers into type real. Most numeric coercions can be omitted in Isabelle:
they are inserted automatically.
But things are delicate in this example, so it’s better to be explicit.
Defining $R$ and $k$
We begin with the theorem statement and the two definitions shown in the blackboard figure:
proposition "sqrt 2 ∉ ℚ" proof define R where "R ≡ {n. n > 0 ∧ real n * sqrt 2 ∈ ℕ}" define k where "k ≡ Inf R"
Already an error: 0 is a natural number, but it needs to be excluded from the set $R$ because otherwise $k=0$ and the argument falls apart.
The traditional proof of irrationality begins by claiming that there are no integers $p$ and $q$ such that $(\frac{p}{q})^2 = 2$. The proof involves simply showing that both $p$ and $q$ would have to be even numbers, while every rational number can be written in the form $\frac{p}{q}$ where $p$ and $q$ are coprime. We could even make a distinction between the rational number $\frac{p}{q}$ and the real quotient $p/q$ in order to prove the theorem in the absence of the reals.
Our proof today begins by finding $p$ and $q$ such that $p/q = \sqrt2$.
assume "sqrt 2 ∈ ℚ" then obtain p q where "q≠0" "real p / real q = ¦sqrt 2¦" by (metis Rats_abs_nat_div_natE) then have "R ≠ {}" by (simp add: R_def field_simps) (metis of_nat_in_Nats) then have "k ∈ R" by (simp add: Inf_nat_def1 k_def) then have kR: "real k * sqrt 2 ∈ ℕ" and "k > 0" by (auto simp add: R_def)
We have already defined $k$ to be the infimum of $R$, but for this to be useful we need to show that the set $R$ is nonempty. It then follows that $k$ belongs to $R$ and satisfies its characteristic properties.
Defining $k’$
The informal proof takes advantage of the typelessness of traditional mathematics (apologies to those offended) by writing the real number $k(\sqrt2-1)$ and showing it to be a natural number: a seamless transition. The Isabelle script begins by calling this quantity $x$ and then, having shown it to belong to ℕ, obtains the corresponding natural number: $k’$. Looking at blackboard carefully, we can see that a few steps have been skipped.
define x where "x ≡ real k * (sqrt 2 - 1)" have "x ∈ ℕ" using ‹0 < k› by (simp add: kR right_diff_distrib' x_def) then obtain k' where k': "x = real k'" using Nats_cases by blast have "k' > 0" using ‹0 < k› k' of_nat_eq_0_iff x_def by fastforce
Showing $k’\in R$
We have already shown that $k’>0$, but the nontrivial part of our task is the third line of the blackboard proof. Breaking it up into stages as shown keeps the proof justifications simple. We could skip some steps, when Sledgehammer would obligingly find a monster proof.
have "real k' * sqrt 2 = 2 * k - k * sqrt 2" by (simp add: x_def algebra_simps flip: k') moreover have "real k' * sqrt 2 ≥ 0" by simp ultimately have "real k' * sqrt 2 ∈ ℕ" by (simp add: kR) with R_def ‹0 < k'› have "k' ∈ R" by blast
Finishing up
Once we can show $k’<k$, the result follows by the minimality of $k$.
have "x < real k" by (simp add: ‹0 < k› sqrt2_less_2 x_def) then have "k' < k" by (simp add: k') then show False using ‹k' ∈ R› k_def linorder_not_less wellorder_Inf_le1 by auto qed
The Isabelle theory file is available to download.
Postscript
This proof assumes a more sophisticated background theory than the traditional one, which would have been a problem 30 years ago when few proof assistants supported the real numbers. A couple of Isabelle formalisations of the traditional proof are available and it’s up to you to decide which approach is clearer.
A previous post discussed reasoning about the least element in the more general context of descriptions, but this example came from the wild (Twitter, anyway).