Isabelle quick start guide
[newbies Isabelle Fibonacci I am often asked, “how do I get started with Isabelle?” For example, why don’t we have an analogue of Kevin Buzzard’s excellent Natural Number Game for Lean? Well, maybe I am lazy, but it’s impossible to re-create the Isabelle experience in a web browser. Instead, we make it easy for you to install Isabelle on your own machine, be it Windows, Linux or Mac, and provide lots of examples to play with. An 8GB Raspberry Pi should be enough to get started.
Put it on your computer
It’s this easy:
- download everything you need with a single click (just choose your platform)
- install in minutes according to the instructions
- launch, on both Windows and macOS after dismissing the built-in protections against Trojans; you can also launch Isabelle from the UNIX command line
But then what? You need some small examples to get a hang of the syntax and then bigger ones to learn how to scale. On this blog, visit the newbies and Isabelle tags.
But now I see that even the simplest example, on Fibonacci numbers, is not really for newbies. The proofs are simple but polished, hiding the trial and error that a beginner would inevitably go through. They are in the structured Isar style, where every claim has a single-line proof, although most real proofs (especially big ones) involve chains of tactic steps such as one finds in other proof assistants such as Lean, Coq and HOL4: so-called apply-style proofs.
Prove something trivial
We begin with the same Fibonacci example as before,
but this time as a true newbie.
First we need a theory declaration specifying
the theory name (which needs to match the file name)
and what it imports, here simply Main, a bare-bones HOL environment.
We supply the definition of the Fibonacci function,
which maps natural numbers to natural numbers (type nat => nat).
Then we state a simple lemma to be proved and type in our very first tactic,
using apply (which is how we can apply a series of tactics one after another).
The side panel displays the two subgoals generated by the tactic.
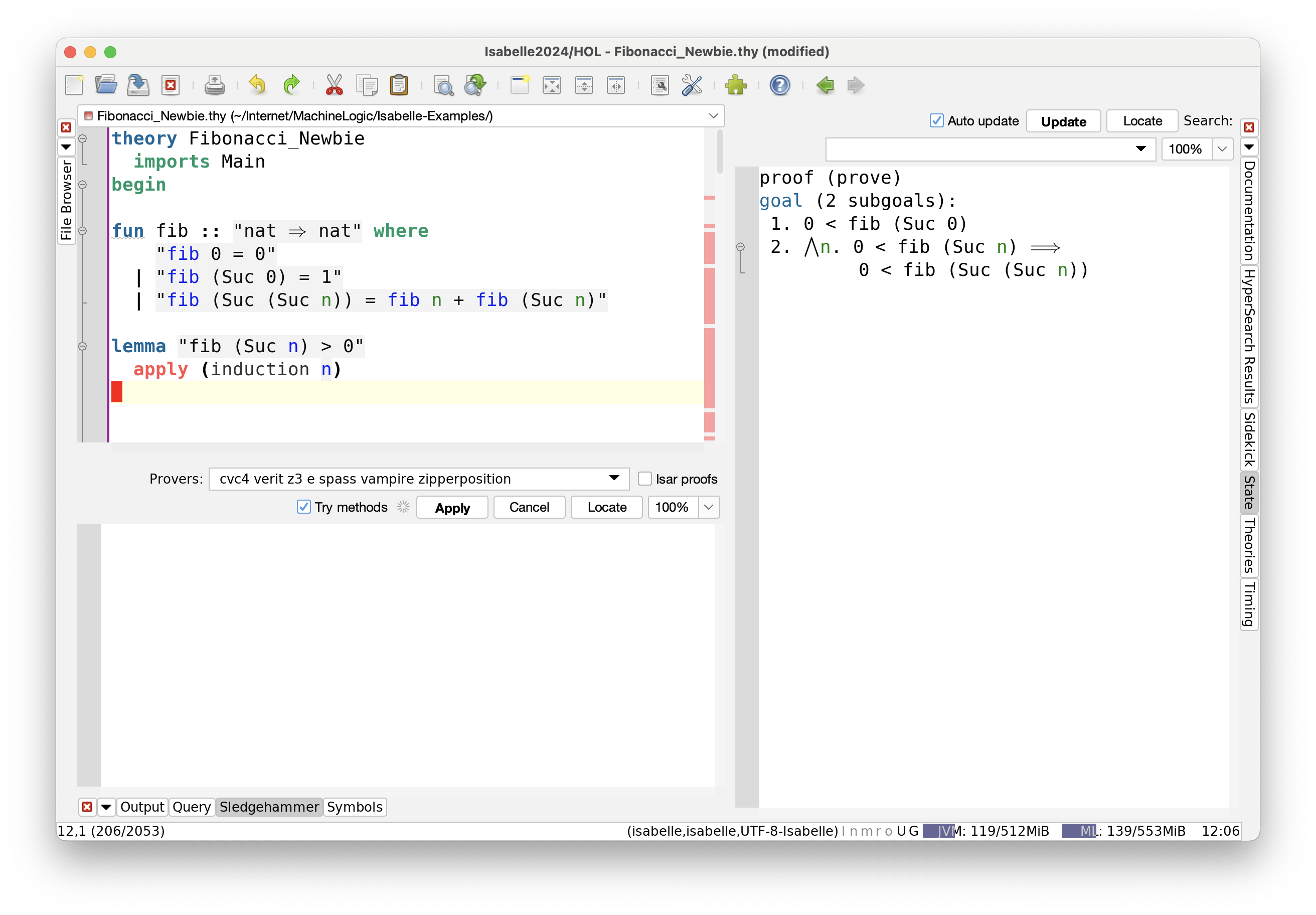
Looking at the subgoals, the second is to prove $F_{n+1} \to F_{n+2}$,
which isn’t ideal. (And don’t be put off by the 0/Suc
notation, which is common in proof assistants and best for this type of work.)
The right form of induction should conform to the definition $F_{n+2} = F_{n+1} + F_n$,
and Isabelle provides it for us, as fib.induct.
We simply add a reference to that in the theory file.
Note that the interface allows you to edit your material willy-nilly, continuously processing it as you type it in.
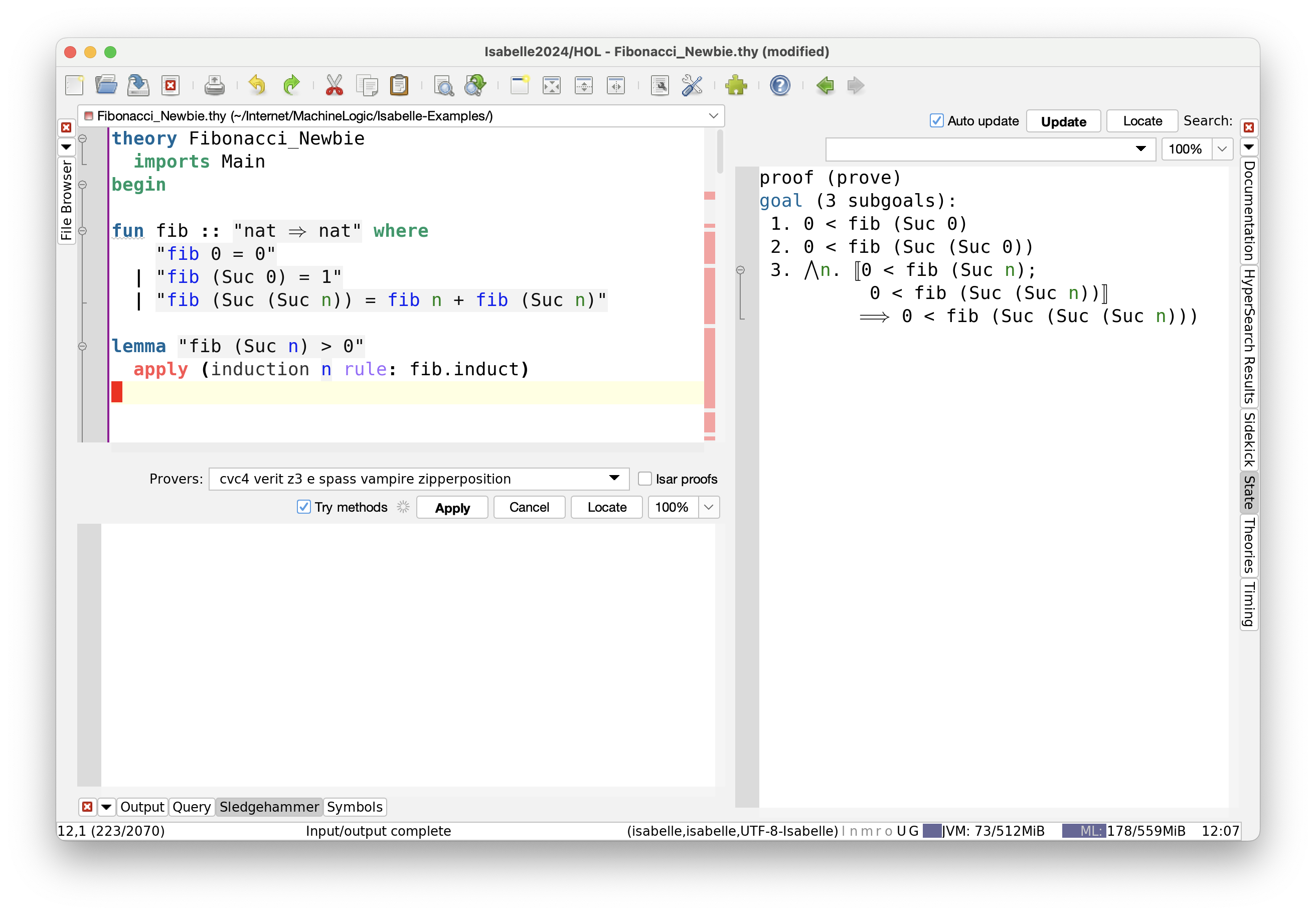
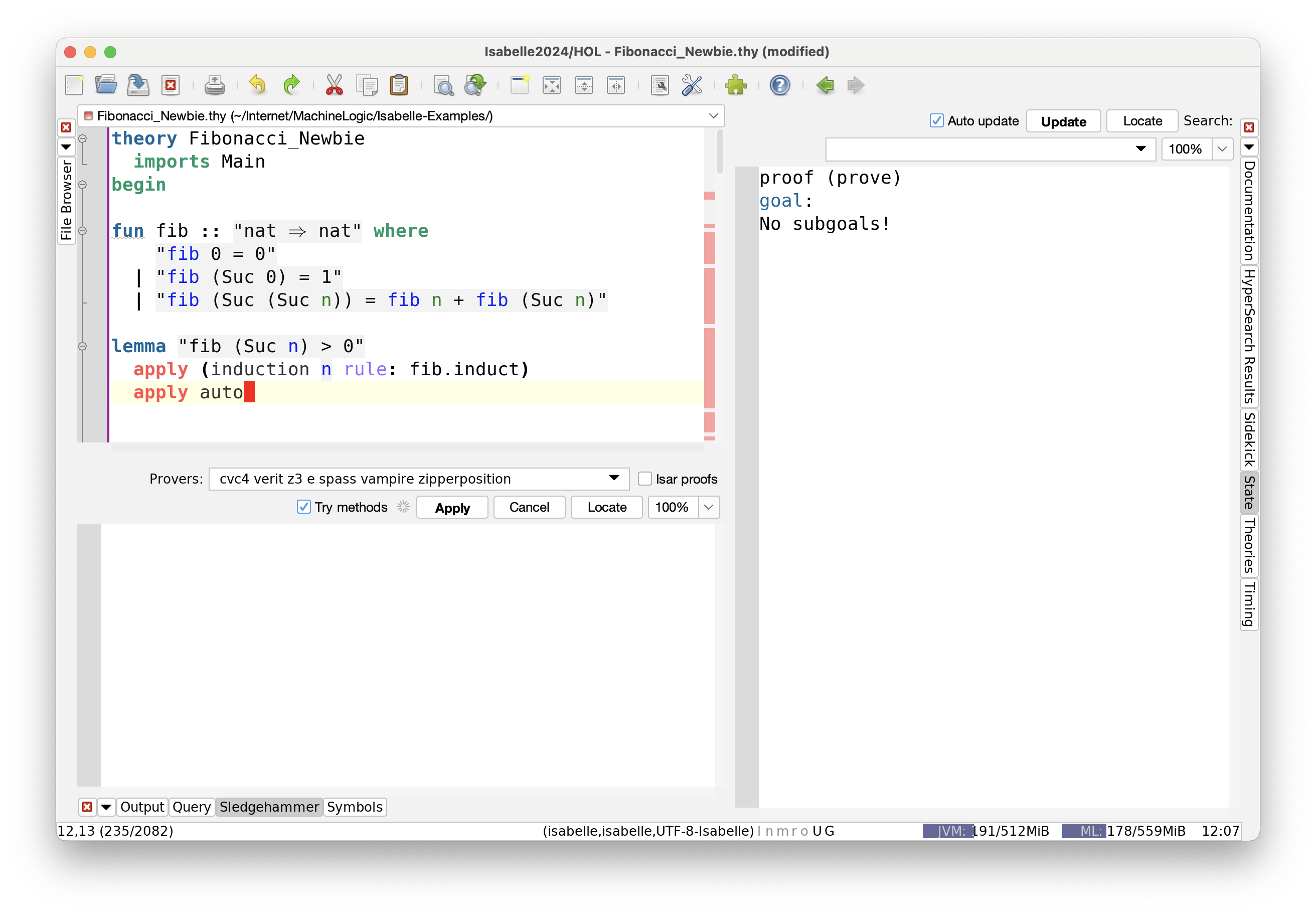
These subgoals look promising, and indeed the auto tactic can finish the job.
It turns out that the ordinary induction rule leads to an equally simple proof – try it –
but only because, due to the types, we get $F_n\ge0$ for free.
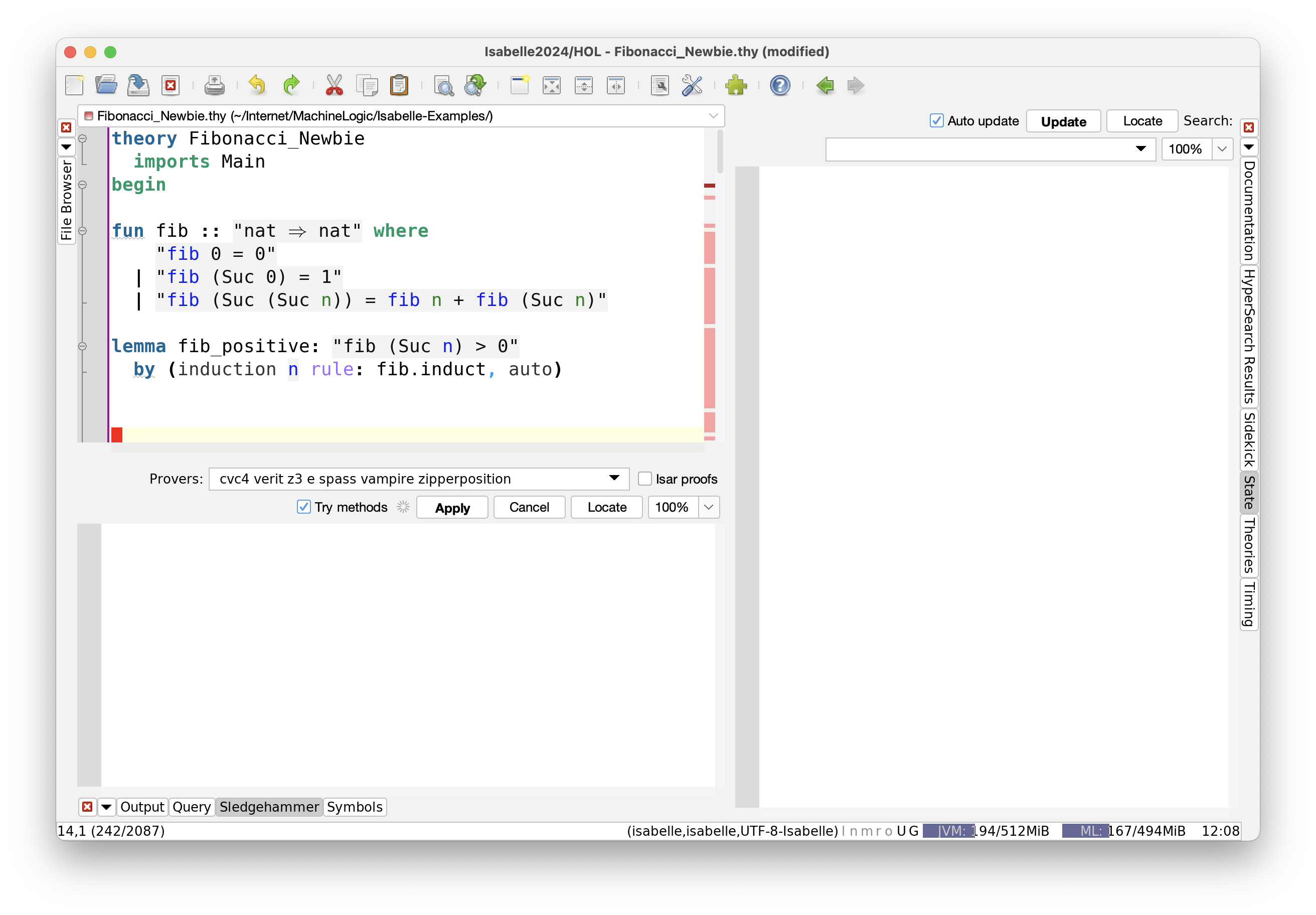
Finally, we can polish the proof, giving it a name and replacing the apply-lines with by and a pair of comma-separated tactics.
Prove something harder
Our second example is a more sophisticated identity about Fibonacci numbers.
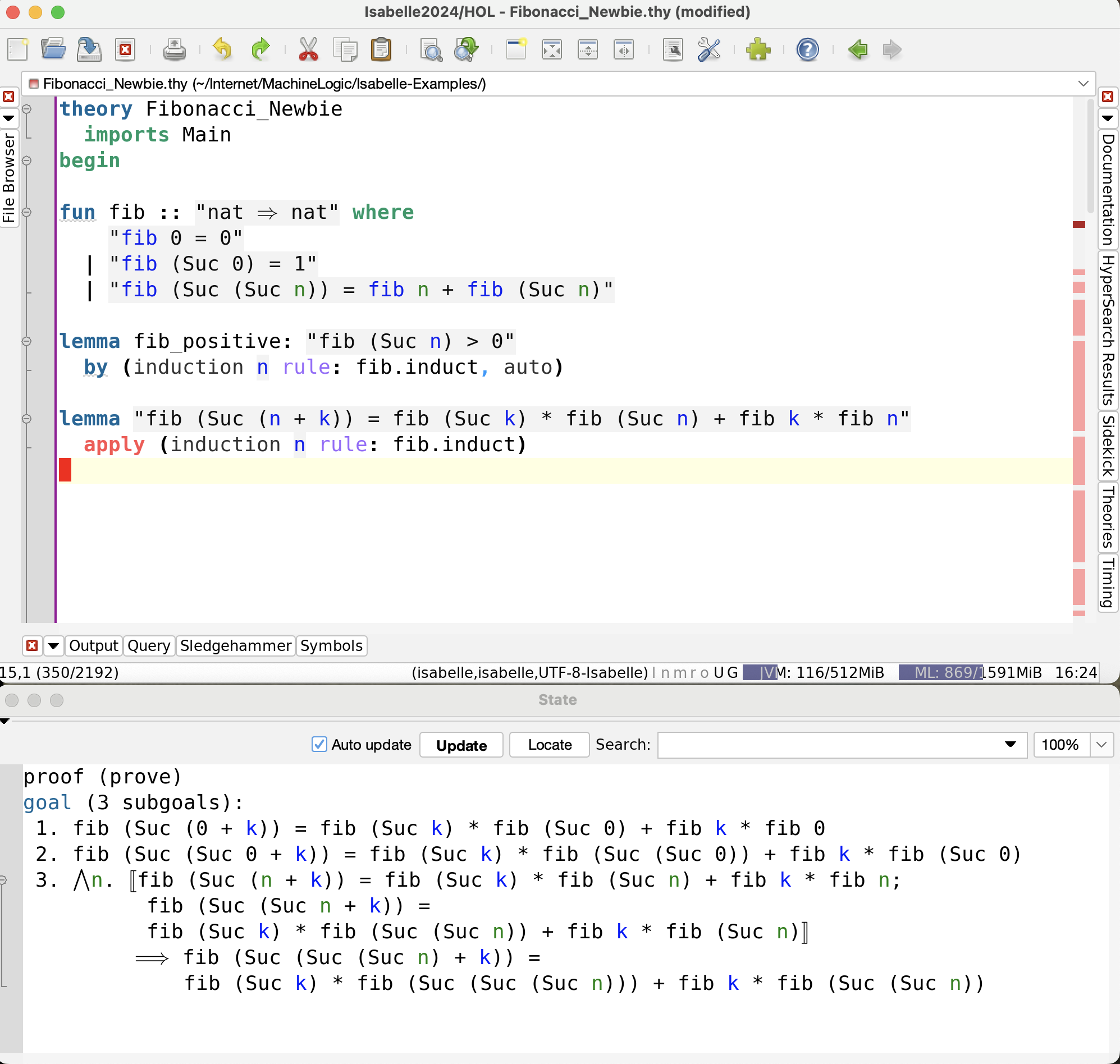
We begin by induction using fib.induct, which worked well last time.
The three subgoals are shown below.
(In a standard Isabelle setup, they would probably appear on the right as before.)
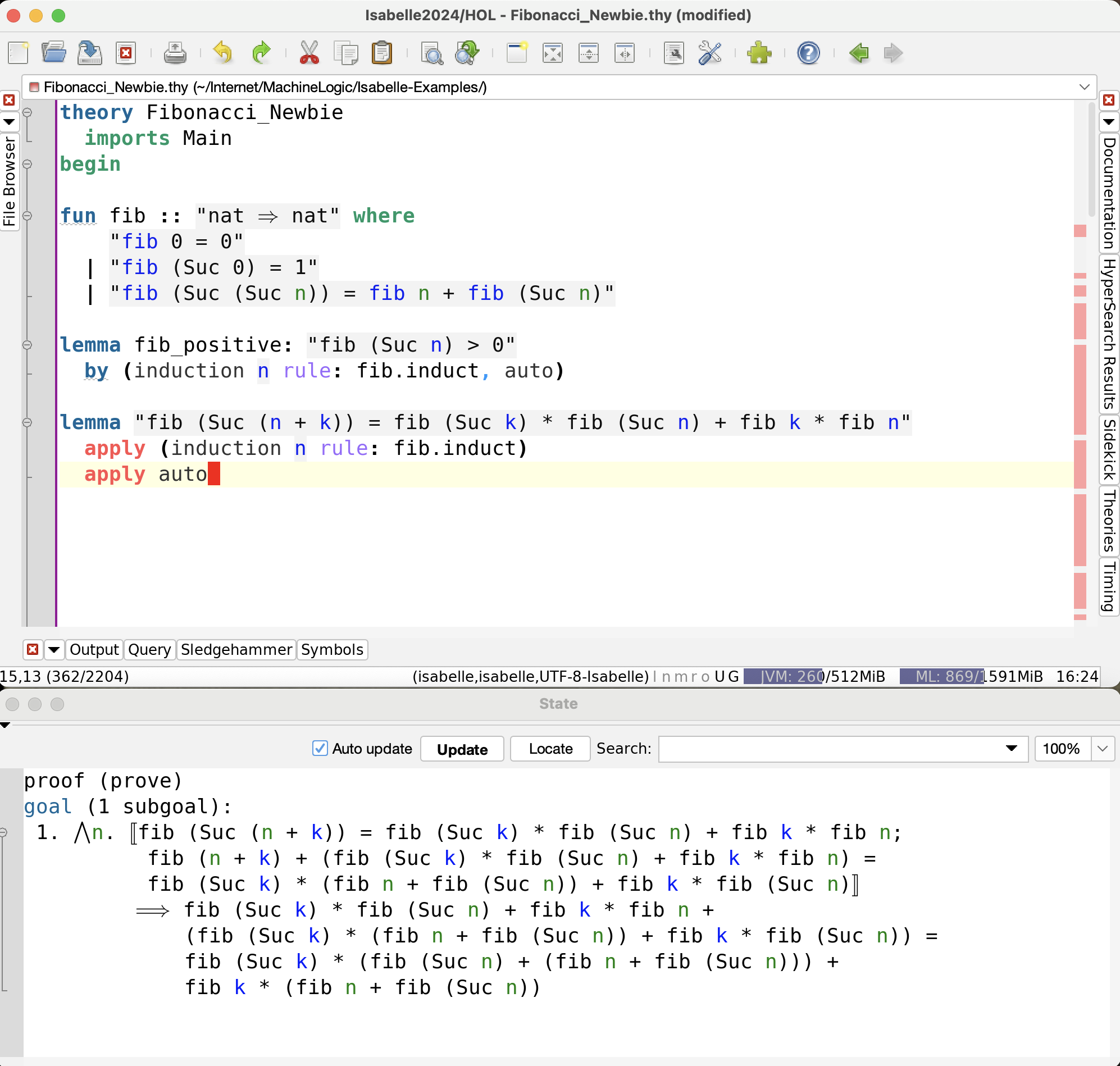
The obvious step to try after doing an induction is auto , so here we go.
The subgoals are again shown below: a stubborn one has survived.
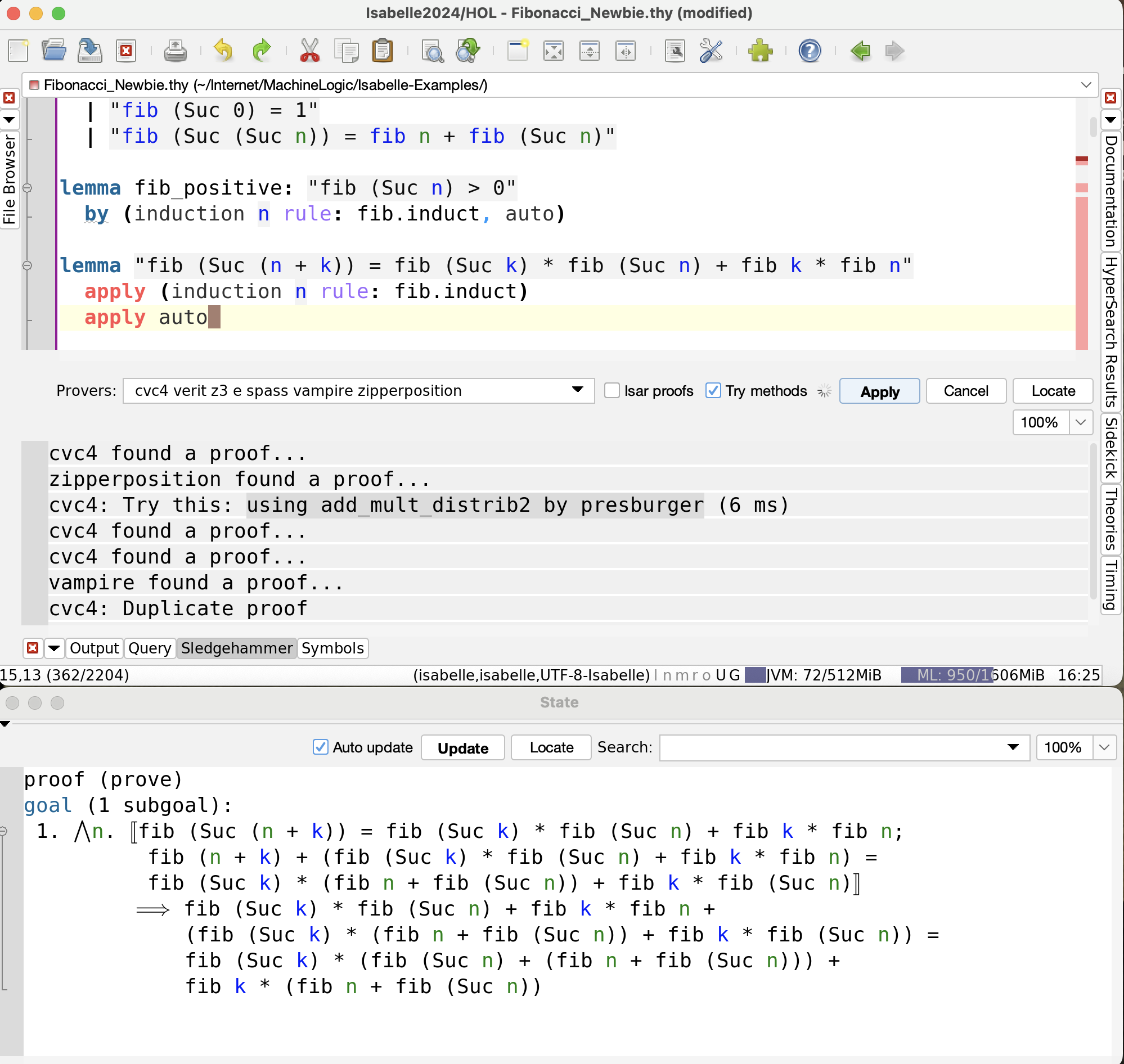
The obvious step to try when an auto is not sufficient is sledgehammer.
We try it now, bringing up the sledgehammer panel and clicking the Apply button.
Sledgehammer quickly comes up with a suggestion:
to use a theorem called add_mult_distrib2, which is a distributive law.
Now all we need to do is click on the highlighted line in the sledgehammer panel,
which will then insert itself right into our proof.
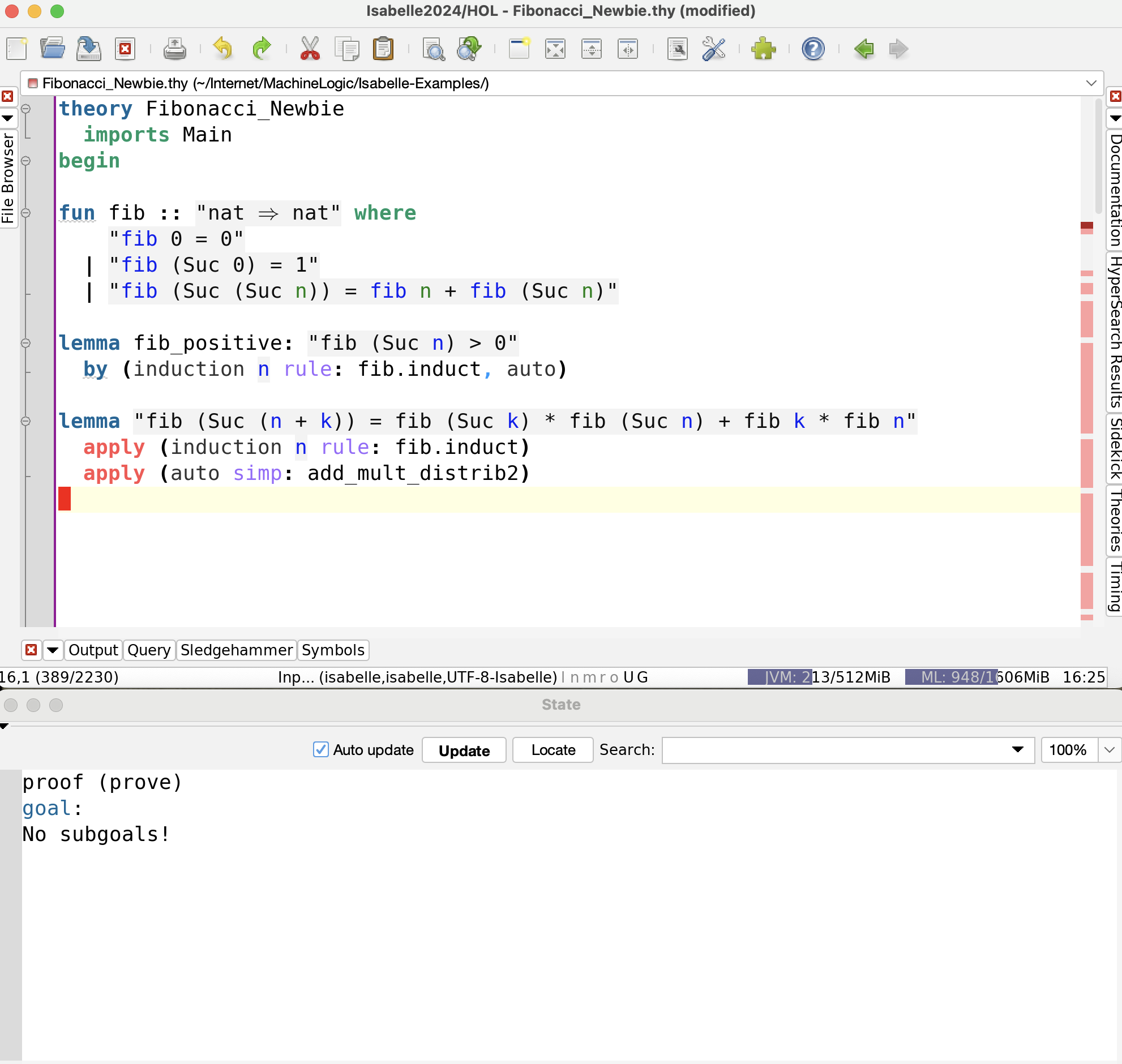
But we can also use the suggested proof as a hint to improve our
auto call, including add_mult_distrib2 as an argument.
As we can see, calling auto in that way proves all three subgoals at a stroke.
To finish this proof, since the pair of tactics is a little too long perhaps to combine into a by-command, we simply terminate the string of apply-lines with done. A long or messy sequence of tactics that does not lend itself to a structured proof is best left in this form.
Prove something even harder
For the third example, let’s see how to write an induction in structured form. Here we want to show that $F_n$ and $F_{n+1}$ are coprime. To start a structured proof, use the keyword proof.
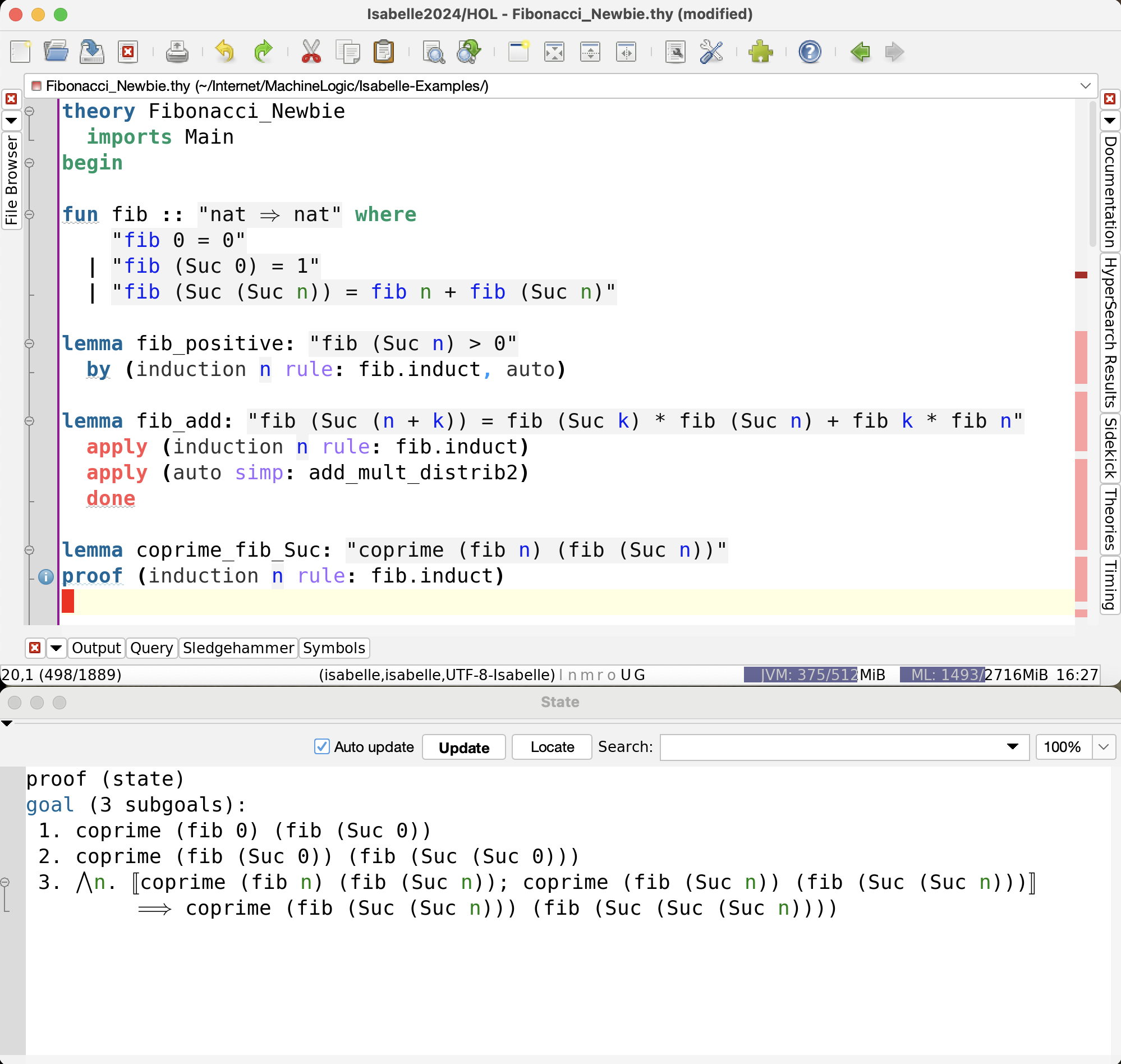
A cool thing about the interface: proofs using induction or cases
automatically generate a structured proof template,
which will insert itself into your theory file.
Simply move your mouse to the faint blue underlining and click on the pop-up.
Below, I have managed to prove the first two cases of the induction
using individual auto calls.
The third is too difficult for auto, but succumbs to sledgehammer.
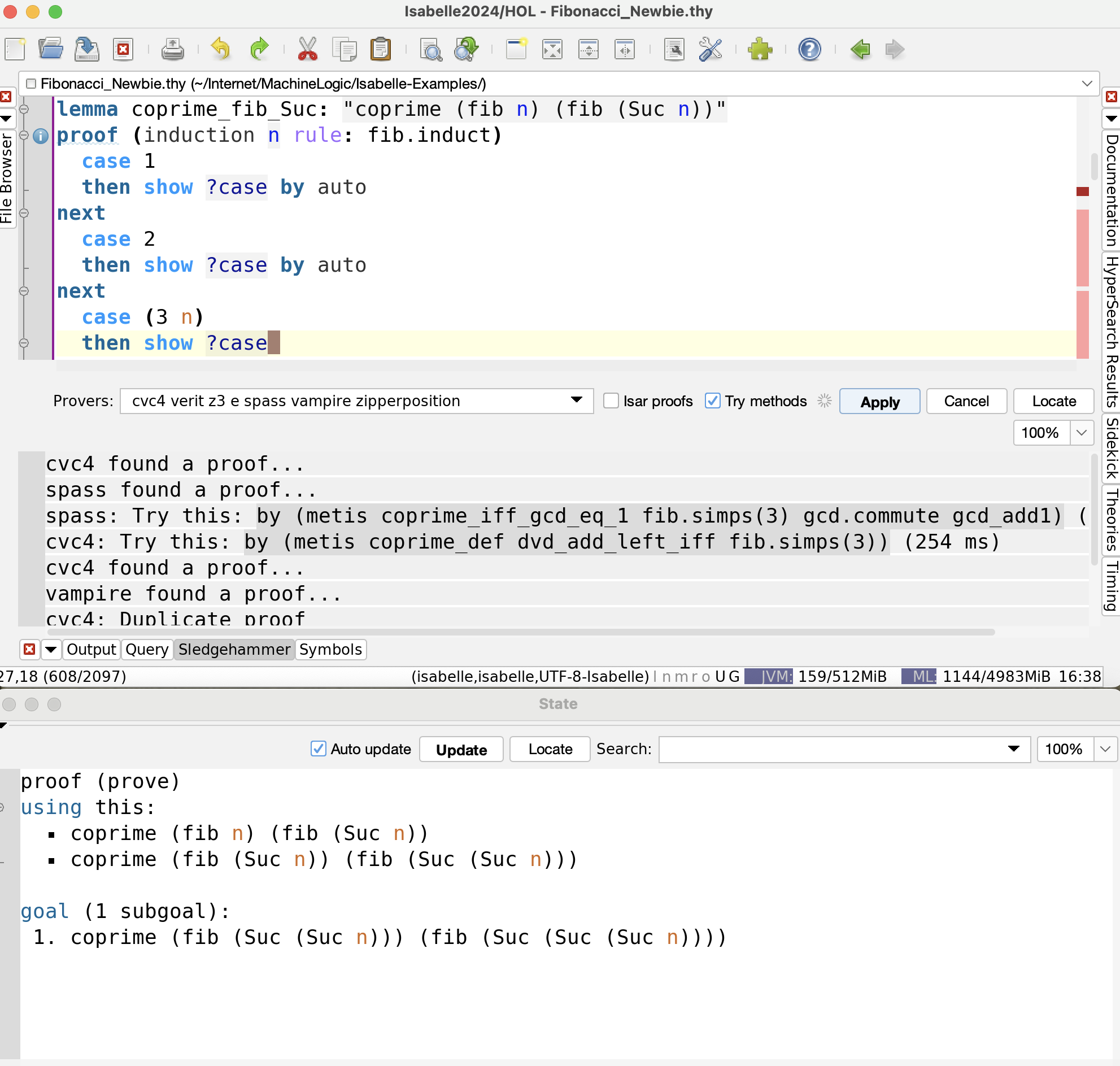
Once again, we can polish this proof. Since auto proves two of the cases, we can delete them and insert auto after the final qed.
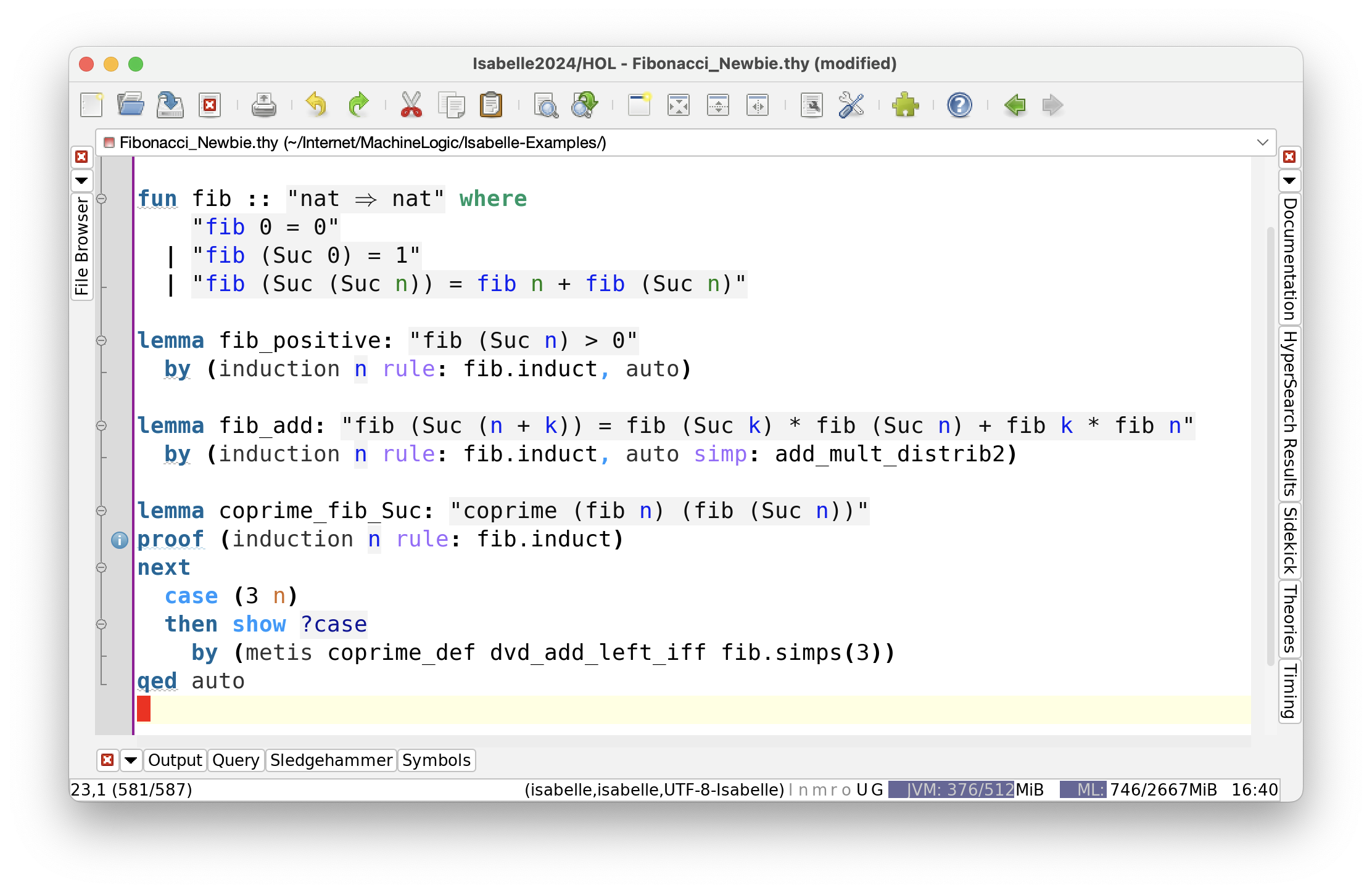
So we have seen in some detail the exploratory steps needed to start a proof. And we’ve also seen the equally necessary step of polishing the final proof, rather than simply quitting once we have proved all the subgoals. As with all forms of code, that it works is not enough: it needs to be readable and maintainable.
To try these examples for yourself, simply
download the original theory file,
which contains the definition of Fibonacci.
You can play around with the existing proofs or write your own.
The proofs presented in this post
can be downloaded directly.
You might also look in the directory HOL/Examples
for examples such as Ackermann’s function
(discussed in this post
and Cantor’s theorem.
After fooling around a little, it will be time for you to read some actual documentation. Take a look at the tutorial Programming and Proving, which is the first one on Isabelle’s documentation page and can also be opened from the Documentation panel of Isabelle itself.