A trickier lower bound proof
[formalised mathematics analysis Last summer, I treated an example of reasoning about a function that contained a (removable) singularity. That post ended with a challenge: to do the same thing for a much trickier function. Last week, Alexander Pach responded with a solution, which I am delighted to present below.
A recap
The task last time was to find the minimum of $x\ln x$ for $x\ge0$. Although strictly speaking it is undefined when $x=0$, it tends to 0 as $x$ approaches 0 from above, and happily, 0 is the value Isabelle attaches to it anyway. We had to show the function’s continuity with separate proofs for the cases $x=0$ and $x>0$. We then obtained its derivative (for $x$ strictly positive) and by elementary reasoning about its sign proved that the desired minimum was $-1/e$.
The challenge
The previous post suggested trying a similar experiment for $x\sin(1/x)$. This function also has a removable singularity at 0 and its continuity proof (in Isabelle) is the same as the one for $x\ln x$. However, this function is a horror:
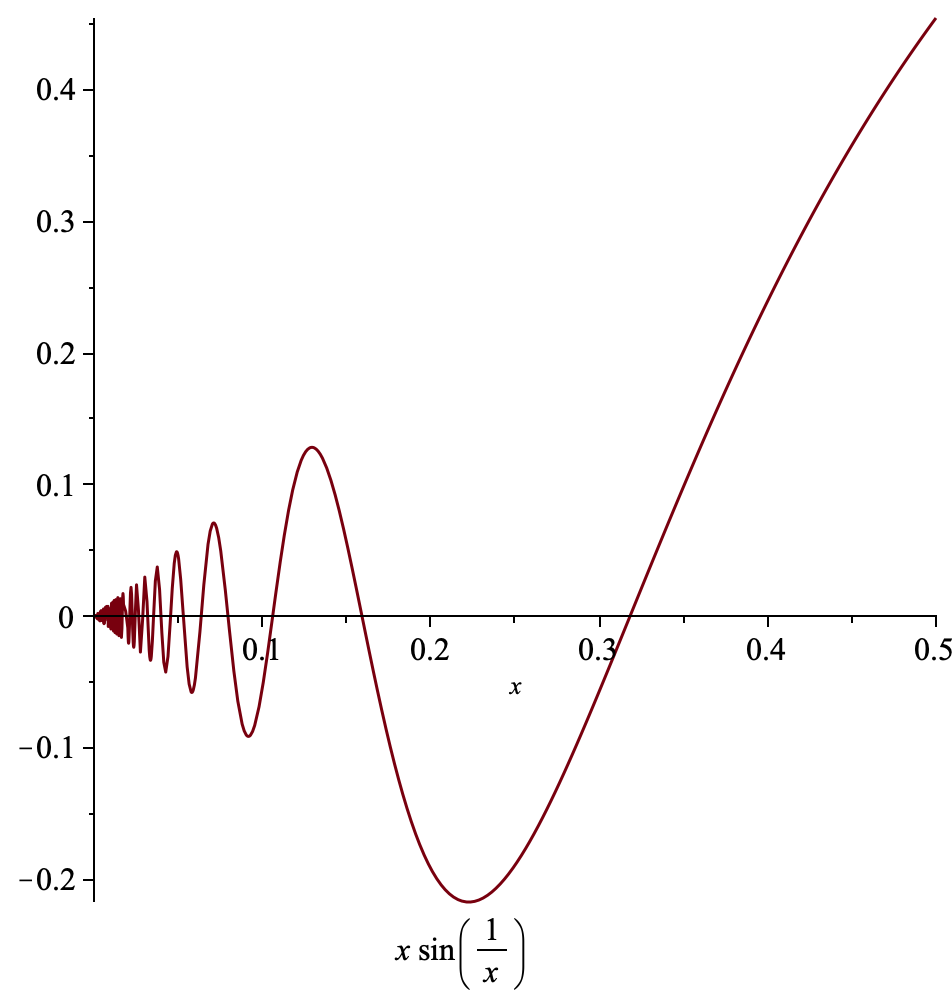
Its derivative, namely $\sin(1/x) - \cos(1/x)/x$, doesn’t look nice either. The lower bound does not appear to be expressible by a simple formula, so Alexander set up a framework for proving that a given number was a lower bound. He then calculated it to 78 decimal places!
-0.217233628211221657408279325562470734223044915435587482365449027714505343589063(39)
You can download his theory here.