Mike Gordon and hardware verification
[MJC Gordon verification HOL system Stanford higher-order logic In the late 1960s, breakthrough papers by Robert W Floyd and Tony Hoare seemed to herald the advent of fully-verified software. Progress soon slowed however. It became clear that once you went beyond a simple flowchart program and had to deal with the horrors of procedures, variable scopes and aliasing, things were not so simple after all. I vividly recall, while still a student at Stanford, spotting a PhD dissertation boldly entitled Hardware Verification, and thinking that the author (Todd Wagner) had to be out of his mind to tackle something surely so difficult. Little did I suspect that I was soon to acquire a friend and colleague, Mike Gordon, who would make hardware verification a reality, and even make it look easy.
Modelling hardware
Sometime early in the 1980s, after I had joined Mike Gordon’s group at Cambridge, he popped into my office and left a preprint entitled something like “A very simple model of CMOS”. (Though I’ve been unable to locate any publication with a similar title.) Shall we work together on this?, he asked. In a fateful decision, I said I would prefer to follow my own path (which at the time meant the automation of type theory), and it’s intriguing to speculate what might have happened if I had said yes. We never published a single joint paper.
Mike’s fundamental discovery, which he had worked towards methodically for a decade, was that hardware circuits could be modelled easily using higher order logic. And his approach worked exactly the same whether the components being combined for individual transistors or were built of thousands of transistors.
His idea was simply this:
- every device modelled by a relation on its ports, describing which combinations of port values were possible
- no distinction between inputs and outputs
- port values could be anything: bits, words, vectors, functions (for time-indexed signals)
- all in a standard formalism, higher-order logic
Here is a device with four ports. We may imagine that $a$ and $b$ are the inputs and $c$ and $d$ are the outputs, but this is not modelled.

The simplest devices include power and ground (represented by T and F), and transistors, such as the following N-channel:
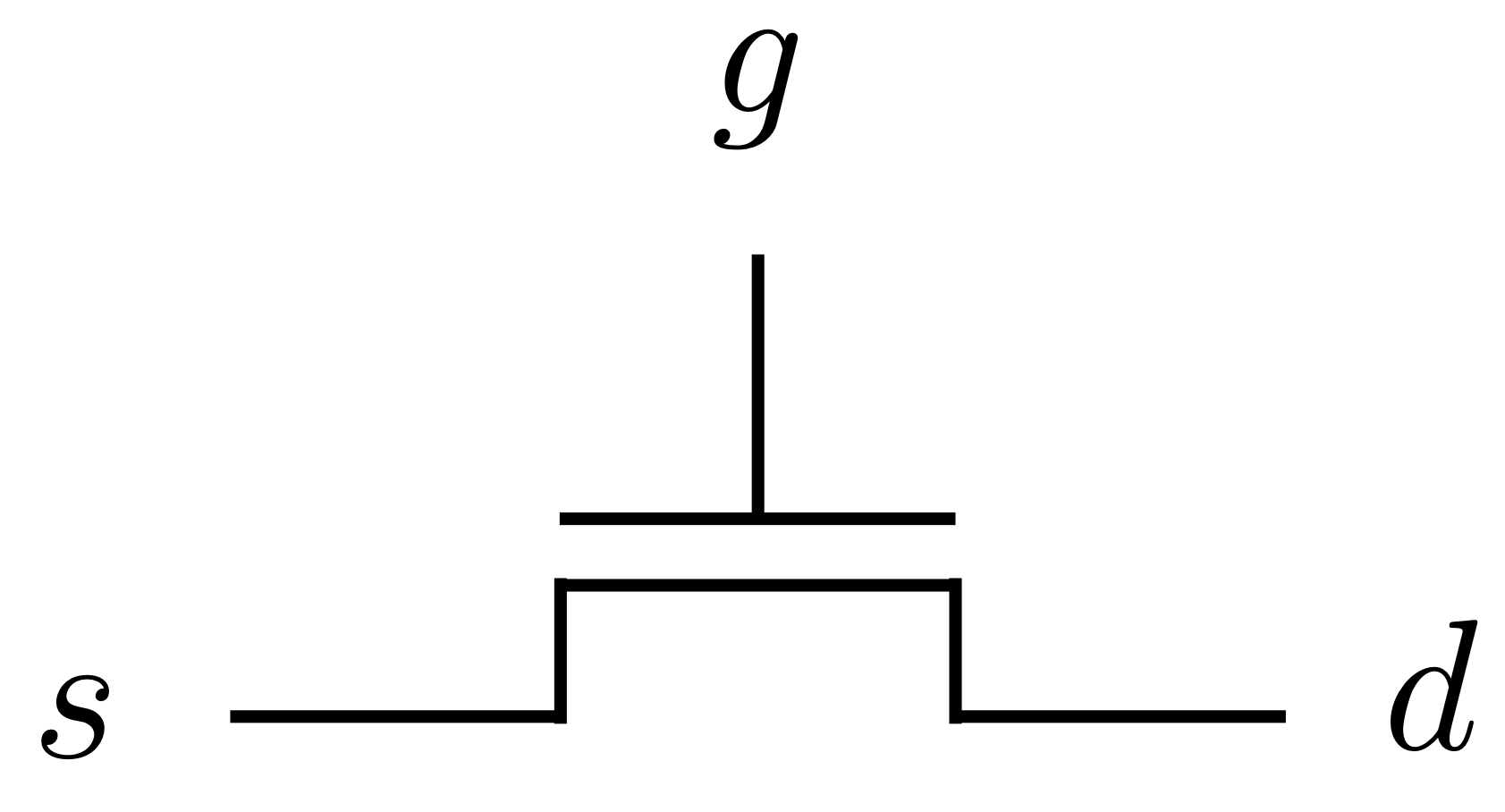
Here we see why the relational model is ideal. The formula for this transistor is $g\to d=s$ and while $g$ is obviously an input, $d$ and $s$ cannot be called either inputs or outputs.
Building circuits from components
The following figure shows two devices connected by a wire. The connected ports must have the same value, while the other ports of each device are constrained by that device alone; we specify this by the conjunction of the two formulas, identifying the connected ports. Now suppose that we wish to hide the connected ports (or indeed any ports). Hiding means the port is no longer available for connection. It’s accomplished by existential quantification over the corresponding variable (since some value certainly “exists”). Relational composition in mathematics is done in exactly the same way.
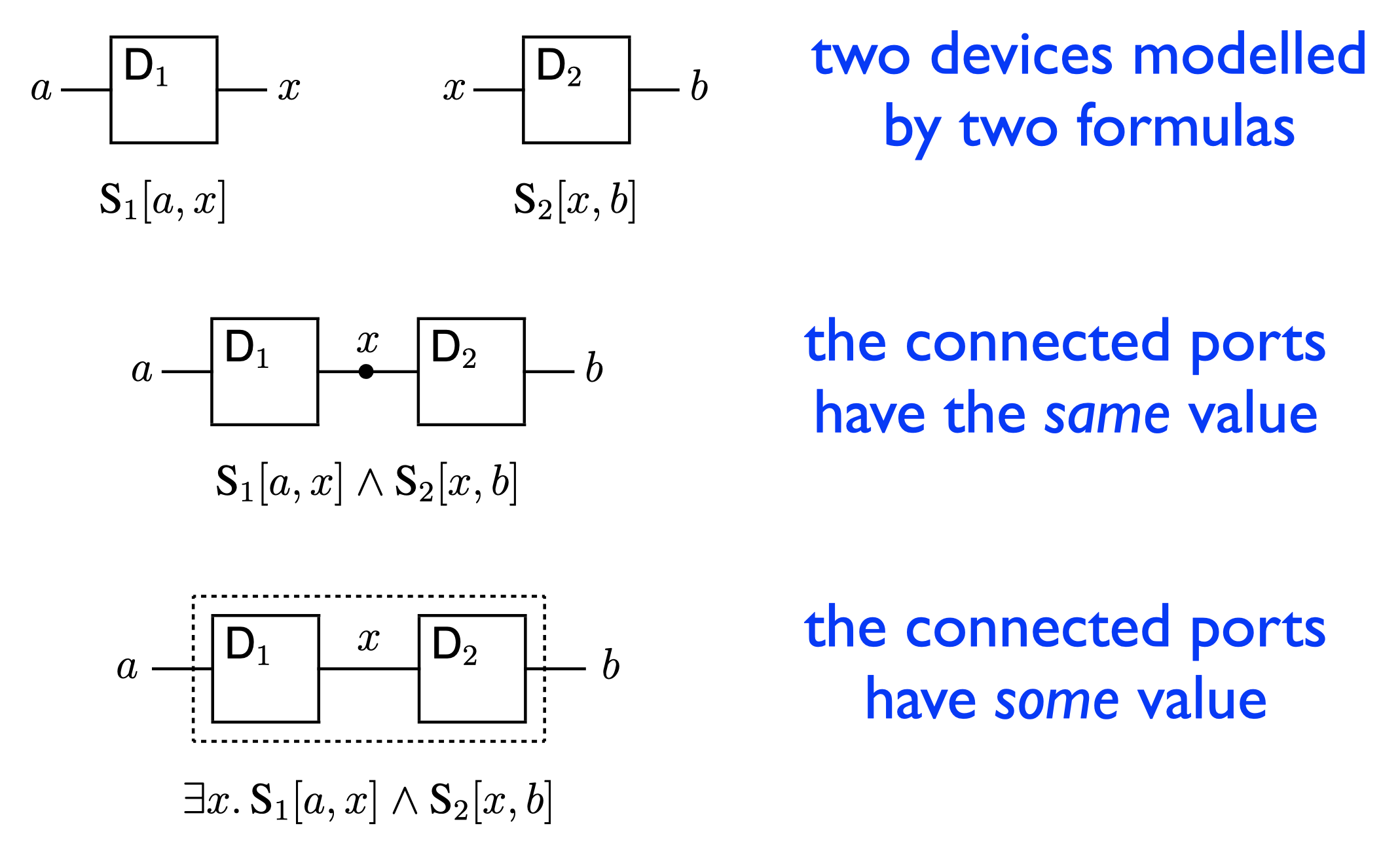
So here is the plan for verifying any hardware device. We specify it by a formula Spec over the variables $a$, $b$, $c$, $d$ describing the behaviour we want. We implement it by means of a circuit consisting of simpler components; from this implementation and the specifications of the simpler components, we obtain (as described above) a formula Imp for the behaviour delivered by the implementation. Then the formula Imp$\to$Spec expresses (for $a$, $b$, $c$, $d$) that every behaviour exhibited by the implementation is allowed by the specification. Now, just prove it. We can go on to implement the simpler components in terms of even simpler ones, for development by refinement.
Short circuits and other issues
This modelling approach is obviously simple, but is it too simple? Mike called Imp$\to$Spec partial correctness (which for software verification refers to correctness under the assumption of termination) because it degenerates to triviality in the presence of a short circuit: an implementation that connects power to ground (because Imp itself would then be F). While nobody would create a short circuit on purpose, it’s not hard to imagine a combination of transistors that could produce one for certain inputs. Given such an input, a real-life implementation would melt, but at least it wouldn’t deliver the wrong answer! Mike Fourman suggests addressing this issue by proving “termination” through some formula of the form $\forall\exists$Imp, asserting that every combination of “inputs” (as we regard them) can be satisfied by some values on the remaining ports. An early paper devotes its final section to this issue.
That aside, every hardware designer can easily see that these models ignore many important design criteria: fan-out (the number of inputs that can be driven by an output), gate delays, capacitance effects, overheating. Designers must continue to rely on their other tools to deal with those issues, relying on verification for the logical functionality alone. Mike’s models have held up well, while more elaborate models such as Glynn Winskel’s (incorporating signal strength) seem not to have caught on.
In a previous post I stated some general principles about modelling. To repeat: models approximate reality, focussing on some particular aspect (in this case, logic) that we need to reason about. Models need to be simple enough that we can understand them, which also means understanding what they can’t do.
Postscript
I have written a scientific biography of Mike Gordon (also here) outlining the history of his work on hardware verification, among much else. It’s interest that Todd Wagner also suggested using logic, but only first-order logic. Mike never mentioned Wagner to me and doesn’t cite him either. And what about software verification? Mike told me that it’s clearly much more difficult than hardware, where interfaces are simple and large devices often consist of a few component types, massively replicated.