Memories: Edinburgh LCF, Cambridge LCF, HOL88
[general Robin Milner MJC Gordon LCF HOL system memories Just over 40 years ago, 2 February 1982, I arrived at Heathrow to take up a postdoc under Mike Gordon and Robin Milner to work on Edinburgh LCF. Mike kindly met me at the airport and drove me to a room that he had organised himself (favours which I have sadly never offered to any of my visitors). This was the true start of my research career, leaving behind my offbeat PhD project and ultimately reconnecting with ideas I had picked up from NG de Bruijn: the formalisation of mathematics. Although I am best known for the development of Isabelle, most of my work in those early years went directly into the HOL system.
Edinburgh LCF
LCF today is best known for its kernel architecture, described in a previous post; Talia Ringer has coined the expression ephemeral proof objects to describe the operation of its kernel, which never actually creates proof objects but could, because the section of the code where proofs can be constructed is strictly confined. Hardly anyone remembers the meaning of the acronym LCF: Logic for Computable Functions. Edinburgh LCF was created in order to carry out proofs in what was then called “fixpoint theory” and was later subsumed into denotational semantics, where it sank out of sight. And it implemented a logic defined by Dana Scott in a paper that he had withdrawn from publication, so you had to get an illicit copy. (It finally appeared in 1993.)
The reference manual was a volume entitled simply Edinburgh LCF. It appeared in Springer’s Lecture Notes series, volume 78; a catalogue listing the titles of every book in the series appeared on the inside covers, something they don’t seem to do any more. Typical books of that era, it is a typescript, very likely generated by nroff.
The radical innovation of LCF was that its metalanguage (ML) would be a full programming language rather than some fixed set of commands. This satisfied the goal of putting automation into the hands of the users while at the same time, through the proof kernel described elsewhere, preventing them from proving $0=1$ no matter how hard they tried. Not that 0 or 1 was actually part of the formalism!
The first part of the book introduces ML, already described as “a general purpose programming language”. Not until page 62 do we reach the LCF formalism, called PPLAMBDA. It’s introduced by the example of proving that if $f(G)=G$ then $\mathop{\textrm{fix}}(f) \sqsubseteq G$.
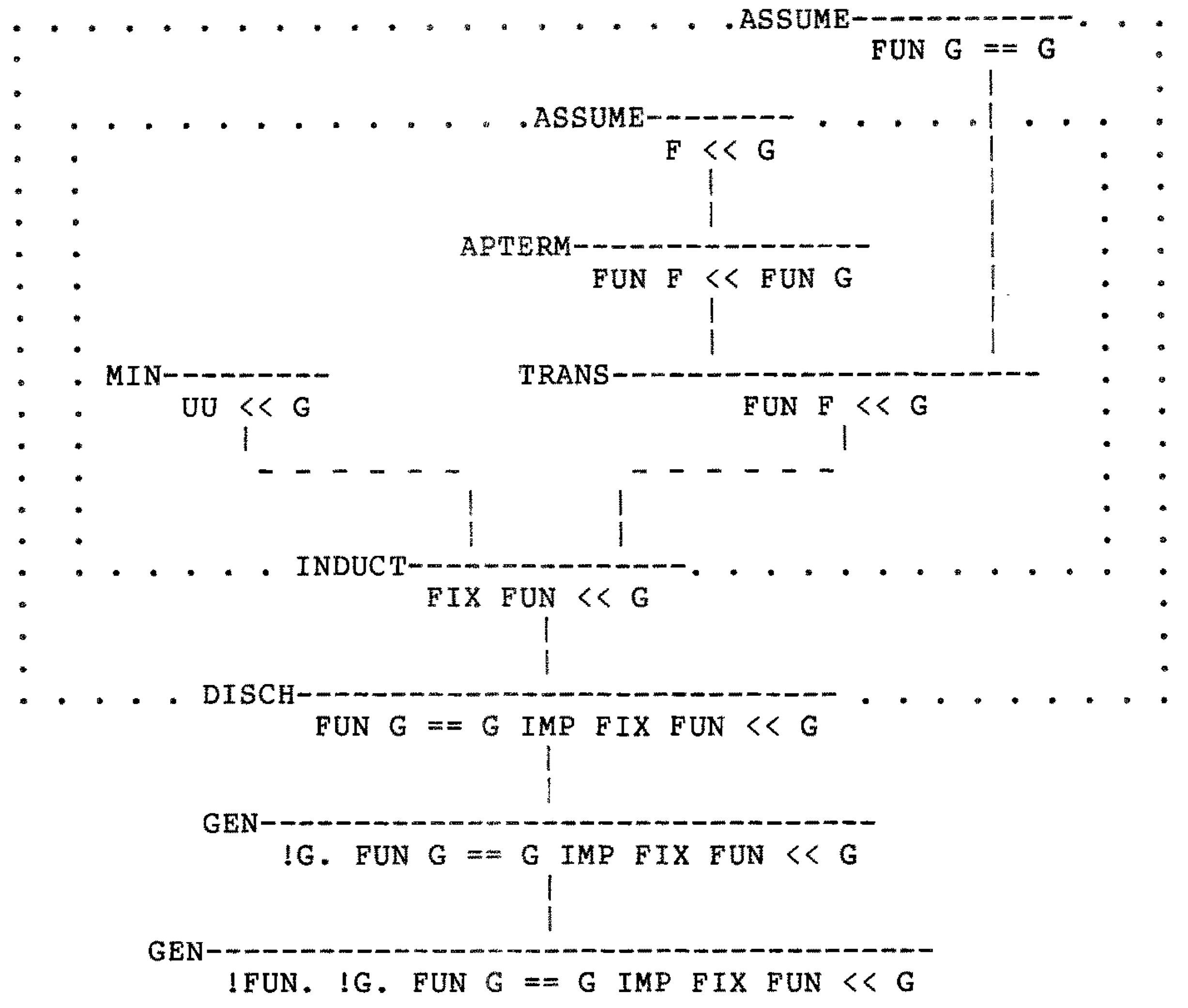
I can remember feeling mixed emotions when reading the manual and experimenting with this system.
- On the one hand, amazement and elation at ML and its polymorphism. Commonplace today in modern offshoots of ML, such as OCaml, and in languages such as Scala, the idea of writing a single piece of code that simply worked for multiple types seemed a miracle.
- On the other hand, disappointment with PPLAMBDA, a tiny fragment of predicate logic with only implication, conjunction and universal quantifiers and the corresponding logical rules.
As types were interpreted by Scott domains, every type contained a “bottom” or “undefined” value, which was written
UU. There was a boolean typetrwith valuesTTandFFfor true and false (as well asUU), and inference rules for case analysis and ex falso quodlibet on booleans (but not for formulas!). That fragment perhaps sufficed for the little examples floating around at the time, but it would be exceeded very quickly.
Extending the logic
If you give somebody the source code, they might want to tinker with it, especially if there’s under 10,000 lines of Lisp and only about 1500 lines of ML. The ML interpreter was naturally written in Lisp, but so were the terms and formulas of PPLAMBDA and the syntactic functions over them. The performance of ML was poor, so it was used only for top level operations: the inference system itself and the backwards proof system built above that.
With the permission of Mike Gordon and Robin Milner, I decided to transform Edinburgh LCF into something bigger. I worked in collaboration with Gérard Huet, who saw in Edinburgh LCF much of value for his own Projet Formel, and I had the pleasure of visiting him at INRIA Rocquencourt on many occasions. We worked on the source code in shifts, a month at a time, mailing magnetic tapes to each other. No git in those days and not much of an Internet either. Completing the logic to full predicate calculus required a bit of coding, trivial by modern standards but complicated by having a single VAX/750 equipped with 4 MB to be shared by the entire department. Please do not romanticise the past.
What did I do for the other months? I had established links with Chalmers University, so I devoted a lot of time to the study of Martin-Löf type theory, intuitionism and related topics. But lo and behold, the first-order inference system I implemented for Cambridge LCF was classical.
Tactic proof
Edinburgh LCF was surprisingly spartan. As mentioned, the only logical connectives it supported were $\forall$, $\land$ and $\to$, but tactics were provided for $\forall$ alone. Looking again at the Edinburgh LCF manual, I see that the first proof (on page 63), corresponding to the diagram shown above, did not use tactics at all but was a purely forward proof using the axioms and inference rules of PPLAMBDA. The theorem was obtained by repeatedly applying inference rules (functions mapping theorems to theorems) to axioms, at the ML level.
The process of doing a tactic proof was simply to bind your formula to an ML identifier, and using what few tactics there were, bind the subgoal list to another identifier and the validation function (necessary to deliver the final conclusion as a theorem) to a third. Then repeat this process for each of the subgoals. At the end of the first tactic proof example (page 66), the manual says
Now the goal list is null, so the composition of our proofs applied to the null theorem list will achieve the main goal.
I recall somebody telling me that you would be so happy that the goal list was null, combining the validation functions would be fun. But one of the first things I did was to devise a simple “subgoal package” that would maintain the current list of goals in a mutable variable and manage the partial proofs internally, so that you could prove everything using tactics alone, and when you had a null subgoal list the theorem you wanted in the first place would just pop out.
Advanced proof tools
I’m grateful to Avra Cohn, Mike’s wife, who was probably the first Edinburgh LCF user and who offered me her library of highly useful functions. I can’t imagine why they were not themselves incorporated into Edinburgh LCF.
She had tactics for the other logical connectives.
She had written ingenious code for combining theorems via pattern matching.
The implication $P\to Q$ justifies both forward chaining (from an
instance of $P$ to the corresponding instance of $Q$)
or backward chaining (reducing a goal that is an instance of $Q$ to the corresponding instance of $P$).
She had implemented a tactic that she called RESTAC, which operated on a set of assumptions and delivered all possible conclusions by forward chaining from the implications there.
There may have been other tactics along those lines.
I took these and added more and unfortunately can no longer remember who wrote what.
But we still have RES_TAC in the HOL family of provers.
And the use of implications for forward/backward chaining is one of the core principles of Isabelle.
Cambridge LCF (and Cambridge ML)
Of course the new system had to be called Cambridge LCF. It comprised 15,000 lines of Lisp and about 4900 lines of ML. People were annoyed with me because I had made tonnes of incompatible changes. (I never could cope with upward compatibility.) So I had to write a new manual, which came out as a book.
Unfortunately, nobody cared about Cambridge LCF because “fixpoint theory” was already as dead as a doornail. The code did not die, however: helped by Gerard I had achieved decent performance for ML, source programs now being transformed into compiled Lisp. Cambridge LCF thus became the basis of many other proof assistants. Mike Gordon used it in his hardware verification developments, first LCF_LSM and then HOL88 (source code available!), keeping the extended tactic library. Gerard Huet used it in early experiments with the calculus of constructions, which ultimately become Coq. The ML subsystem, known as Cambridge ML, was also the basis of the original version of Nuprl.
Postscript
You’ll find more details in Mike’s paper “From LCF to HOL: a short history”, Proof, Language, and Interaction: Essays in Honour of Robin Milner 169–185. Available for free here.)